Для строительства детской площадки рабочие проводили измерительные работы. Они подготовили две площадки квадратной формы. Найди их периметр если известно что величина периметра каждого из них меньше 90 метров. Если цифры в записи одного периметра поменять местами, то получится периметр второго участка
.
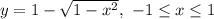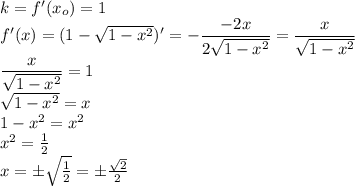
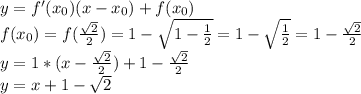
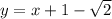и окружности и является искомым значением параметра а: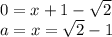
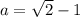
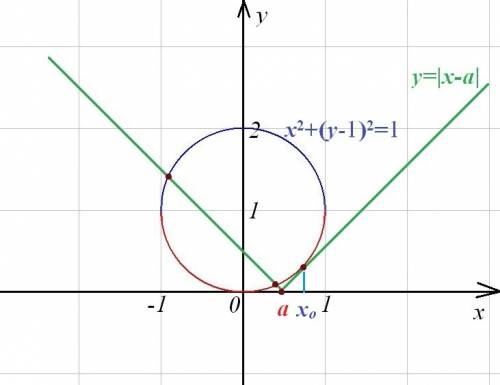
Пошаговое объяснение:
периметр квадрат- это сумма 4 его сторон, значит, число должно делиться на 4. Причем, обе цифры делиться на 4 должны, раз меняем их местами
Получаются цифры 4 и 8. Значит, числа 48 и 84: 48 периметр меньшего, 84м периметр большего
Подробнее - на -