1) Найти производную функции:
А) f ( x )=3 x3+5 x2−4 x
Б) f ( x )=8√ x−cos x
В) f ( x )=(4 x−1 )(6 x+3)
5 x−2
Г) f ( x )=
x3
Д) f ( x )=(2 x−5)6
2) Дана функция f ( x )=sin x. Найдите производную функции в точке x0=−π
3) Найдите уравнение касательной к графику функции f ( x )=2 x3−3 x2 в точке x0=3
4) Дана функция f ( x )=x3− x2−x+2
А) Найдите точки экстремума
Б) Найдите наибольшие и наименьшее значение функции на отрезке
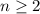равных частей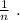
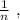нужно разрезать верёвочку длины 2 на 
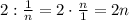частей.
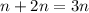частей.
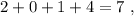не делится на три.
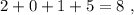не делится на три.
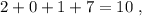делится на три!
не делится на три.
не делится на три.
Dв-?
1) Lа = пDа - длина окружности большой монетки.
2) 2•Lа - длина пути, проделанной меткой на большой монетке, совершившей 2 оборота.
3) Lв = пDв
Меньшая монетка должна для того, чтобы метки совпали, совершить также полное число оборотов. То есть число оборотов должно быть натуральным числом к, причем к>2,
2•Lа = к•Lв
2пDа = кпDв
Число п в обеих частях уравнения можно сократить.
2Dа = кDв
Dв = 2Dа/к
Рассмотрим случаи, когда количество оборотов малой монетки к= 3; 4; 5:
Dв1 = 2•18/3 = 12 мм - первый возможный диаметр монетки в.
Dв2 = 2•18/4 = 9 мм - второй возможный диаметр монетки в.
Dв3 = 2•18/5 = 7,2 мм - третий возможный диаметр монетки в. Но такой диаметр монетки вряд ли возможен.
ответ: 12 мм или 9 мм.