ответ:250 с
Пошаговое объяснение:
Записываем все страницы в книге как 100%.
Поскольку в первый день ученик прочитал 30% книги, значит после этого ему осталось прочесть:
100% - 30% = 70% книги.
Таким образом, во второй день он прочитал:
70% * 40% / 100% = 2800 / 100 = 28% (от всей книги).
Из этого следует, что в третий день процент страниц, которые прочел ученик был равен:
70% - 28% = 42%.
Данное процентное значение соответствует 105 страницам, поэтому всего в книге было:
105 / 42% / 100% = 105 / 0,42 = 250 страниц.
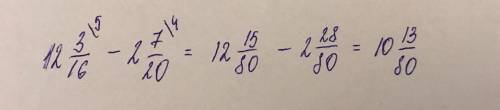
Как составить уравнение биссектрисы треугольника по координатам его вершин Используя уравнение биссектрисы угла:
Пример.
Даны вершины треугольника A(-5;4), B(7;-1) и C(3;10).
1) Составить уравнение биссектрисы треугольника ABC, выходящей из вершины A.
2) Найти длину этой биссектрисы.
1) Угол A образован прямыми AB и AC. Составим уравнения этих прямых.
Уравнение прямой, проходящей через две точки, можно найти, например, по формуле
Уравнение прямой AB:
Уравнение прямой AC:
Подставляем уравнения прямых AB и AC в формулы уравнения биссектрис угла:
и
то есть
и
Из этих уравнений является уравнением биссектрисы внутреннего угла BAC треугольника, другое — биссектрисой внешнего угла при вершине A. Как отличить уравнение биссектрисы внутреннего угла?
Точки B и C лежат по одну сторону от биссектрисы внешнего угла, поэтому при подстановке координат B и C в уравнение мы получим числа одинакового знака. От биссектрисы внутреннего угла B и C лежат по разные стороны, поэтому подстановка их координат в уравнение биссектрисы внутреннего угла даёт нам числа разных знаков.
Подставляем в уравнение x-8y+37=0 координаты B и C.
B(7;-1): 7-8·(-1)+37>0
C(3;10): 3-8·10+37<0.
Таким образом, уравнение x-8y+37=0 является уравнением биссектрисы AF треугольника ABC.
2) Чтобы найти длину биссектрисы, найдём точку пересечения прямых AF и BF.
Уравнение прямой BC:
Координаты точки пересечения прямых AF и BC находим из системы уравнений
Решение системы —
Длину биссектрисы AF находим по формуле расстояния между точками A и F:
Пошаговое объяснение:
Как составить уравнение биссектрисы треугольника по координатам его вершин Используя уравнение биссектрисы угла:
Пример.
Даны вершины треугольника A(-5;4), B(7;-1) и C(3;10).
1) Составить уравнение биссектрисы треугольника ABC, выходящей из вершины A.
2) Найти длину этой биссектрисы.
1) Угол A образован прямыми AB и AC. Составим уравнения этих прямых.
Уравнение прямой, проходящей через две точки, можно найти, например, по формуле
Уравнение прямой AB:
Уравнение прямой AC:
Подставляем уравнения прямых AB и AC в формулы уравнения биссектрис угла:
и
то есть
и
Из этих уравнений является уравнением биссектрисы внутреннего угла BAC треугольника, другое — биссектрисой внешнего угла при вершине A. Как отличить уравнение биссектрисы внутреннего угла?
Точки B и C лежат по одну сторону от биссектрисы внешнего угла, поэтому при подстановке координат B и C в уравнение мы получим числа одинакового знака. От биссектрисы внутреннего угла B и C лежат по разные стороны, поэтому подстановка их координат в уравнение биссектрисы внутреннего угла даёт нам числа разных знаков.
Подставляем в уравнение x-8y+37=0 координаты B и C.
B(7;-1): 7-8·(-1)+37>0
C(3;10): 3-8·10+37<0.
Таким образом, уравнение x-8y+37=0 является уравнением биссектрисы AF треугольника ABC.
2) Чтобы найти длину биссектрисы, найдём точку пересечения прямых AF и BF.
Уравнение прямой BC:
Координаты точки пересечения прямых AF и BC находим из системы уравнений
Решение системы —
Длину биссектрисы AF находим по формуле расстояния между точками A и F: