а) V= abс ( где а - длина комнаты,b-ширина комнаты,с-высота комнаты)
V= 7 м × 5 м × 3 м
V= 105 м³
S=abc (где а-длина комнаты,b-ширина комнаты,с-высота комнаты)
S=7 м × 5 м × 3 м
S=105 м²
ответ:Объем комнаты равен 105 м³,площадь комнаты равна 105 м².
б) Для того чтобы найти объем,нам нужно найти длину → чтобы найти длину,нужно площадь разделить на ширину.
→ а= S|b (где а - длина комнаты,b-ширина комнаты)
→ a = 12 м² ÷ 3 м = 4 м (длина комнаты);
Чтобы найти объем ,нужно умножить высоту,длину и ширину.(V=a×b×h,где h -высота)
V = abh
V = 4 м × 3 м × 2 м
V = 24 м³
ответ:Объем комнаты равен 24 м³.
в)Находим высоту комнаты,зная площадь и объем комнаты.
→ V = h × S , следовательно
Чтобы найти высоту комнаты,нужно объем разделить на площадь.
(h=V|S).
h = 45 м³ ÷ 15 м²
h = 3 м
ответ: Высота комнаты равна 3 м.
Пошаговое объяснение:
а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)
второй - табличный = sinx + C = 0 в подстановке.
ответ: pi* e^(pi)
б) занесу cosx под дифференциал
cosxdx = d ( sinx + 1)
дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0
в) опять под дифференциал
d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)
дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 - 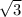
г) под дифференциал:
d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)
дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5
ответ:кай сыныпсын
Пошаговое объяснение: