Дифференциальным уравнением первого порядка называется уравнение вида
F(x, y, y
′
) = 0, (0.1)
в котором x — независимая переменная, y(x) — неизвестная функция. Дифференциальным уравнением первого порядка, разрешенным относительно
производной, называется уравнение
dy
dx = f(x, y). (0.2)
Правую часть уравнения (0.2) будем считать определенной на некотором открытом множестве D плоскости (x, y). Иногда уравнение (0.2) записывают
в виде
M(x, y) dx + N(x, y) dy = 0 (0.3)
и называют уравнением первого порядка, записанным в дифференциалах.
Решением уравнения (0.2) (или (0.3)) на интервале I оси x называется
любая дифференцируемая функция y = φ(x), которая при подстановке в
уравнение обращает его в тождество на I . Общим решением уравнения (0.2)
называется множество всех его решений. Общее решение зависит от одной
произвольной постоянной C и дается формулой
y = φ(x, C). (0.4)
Выражение вида
Φ(x, y, C) = 0, (0.5)
из которого y определяется неявно как функция от x называется общим
интегралом уравнения (0.2).
Решить уравнение (0.2) означает найти его общее решение или общий интеграл. При этом предпочтение, как правило, отдается более компактной записи ответа.
Формы записи уравнения в виде (0.2) или (0.3) равносильны и из одной
записи можно получить другую. Однако, в некоторых случаях, форма записи (0.3) оказывается предпочтительнее, так как в нее переменные x и y входят симметрично. Поэтому, если независимую переменную и искомую функцию поменять местами (разрешить уравнение относительно dx
dy ), то общее решение x = ψ(y, C) полученного уравнения определит
Пошаговое объяснение:
sin (60°) = sin (π/3) = (√3)/2.
Пошаговое объяснение:
Синус — одна из тригонометрических функций, обозначется sin.
В прямоугольном треугольнике синус острого угла равен отношению катета, лежащего напротив этого угла (противолежащего катета), к гипотенузе.Значения синусов для часто встречающихся углов (π — число пи, √ — корень квадратный)
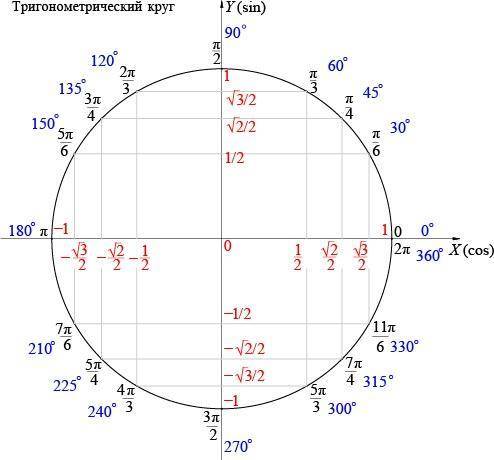
Также значение синуса 60 градусов можно узнать по тригонометрической окружности (или кругу, как его еще называют).
Все значения синуса на тригонометрической окружности расположены на оси ординат. Вычислим значение синуса от 60 градусов.
Найдем на окружности значение аргумента синуса — 60 градусов. Далее опустим перпендикуляр на ось ординат и получим значение  . Таким образом, синус от 60 градусов равен
. Таким образом, синус от 60 градусов равен  .
.
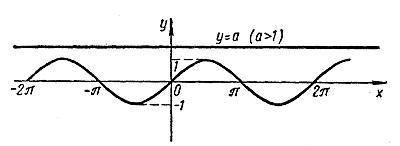
По графику синуса (синусоиде) также можно найти значение синуса 60 градусов. Но для этого иметь хотя бы поверхностные знания о расположении основных значений углов и значений функции синус на координатных осях.
просто посмотреть значение в таблице.
<В = <D = 60 град.
Пошаговое объяснение:
Данный треугольник равносторонний. В равностороннем треугольники все углы равны, поэтому 180:3=60