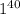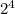Після підключення України до системи обміну інформацією з Інтерполом на першому етапі кількість обмінів була на 666 обмінів менша, ніж на другому. Загальна кількість обмінів склала 2780.
Для оцінки ефективності програми визначте кількість обмінів інформацією на першому та другому етапах. У скільки разів збільшилася кількість обмінів для першого та другого етапів в порівнянні з ситуацією до запуску системи, якщо кількість обмінів за такий самий період до запуску складала 50?

👇

Открыть все ответы

Ответ:

SirenaLi27

04.09.2020

Нет, такого соотношения нет. Так, если это 40 единиц и 4 двойки, то сумма всех числе будет равна 1*40+2+2+2+2=48, а произведение этих чисел $1^{40}$ * $2^{4}$ =16, в этом случае сумма в три раза больше произведения. Наиболее приближены к данному соотношению числа 14 и 15.Так, если это 43 единицы и 15 , то сумма всех числе будет равна 1*43+15=58, а произведение этих чисел 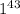$1^{43}$ *15=15, соотношение 58/15= 3 цел. и 13/15. Если это 43 единицы и 14 , то сумма всех числе будет равна 1*43+14=57, а произведение этих чисел 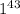$1^{43}$ *14=14, соотношение 57/14=4 цел. и 1/14. Ровно 1 к 4 соотношения нет.

4,4(9 оценок)

Ответ:

Tittans7

04.09.2020

Если среди этих чисел могут быть одинаковые, то можно: возьмем 41 единицу и 2, 2, 3. Тогда сумма равна 1+...+1+2+2+3=48, а произведение 1*...*1*2*2*3=12, при этом 48=4*12.

Если числа различные, то такое невозможно. Вначале докажем, что сумма любых чисел больших или равных 2 не превосходит их произведения. Пусть S(k) - сумма k чисел, каждое из которых не меньше 2, а P(k) - их произведение. Заметим, что P(k)≥2. Сделаем индукцию по количеству слагаемых. S(1)=P(1). Предположим, что выполнено S(k)≤P(k). Тогда, если b - это k+1-ое число, то S(k+1)=S(k)+b≤P(k)+b≤P(k)*b=P(k+1). Здесь неравенство P(k)+b≤P(k)*b верно, т.к. его можно переписать в виде (P(k)-1)(b-1)≥1, что выполняется при P(k)≥2 и b≥2. Теперь, если среди наших 44 чисел имеется только одна единица (а это так, если числа различны), то получаем 1+S(43)≤1+P(43)<4*1*P(43)), т.е. сумма всех чисел строго меньше чем четырехкратное их произведение. Значит равенства быть не может.

4,8(51 оценок)

Это интересно:

11.11.2020

Основные принципы полезной агрессии: как стать более уверенным в себе...

29.07.2022

Как легко и просто найти общий язык с застенчивым парнем, которого вы почти не знаете...

Компьютеры-и-электроника

19.03.2023

Как бесплатно создать сайт: подробный обзор лучших сервисов для начинающих...

Финансы-и-бизнес

23.11.2020

Как купить себе частный остров: преимущества и нюансы покупки...