Sбок = 32(1 + √2) см²
Пошаговое объяснение:
Если две грани пирамиды перпендикулярны плоскости основания, то их общее ребро перпендикулярно плоскости основания.
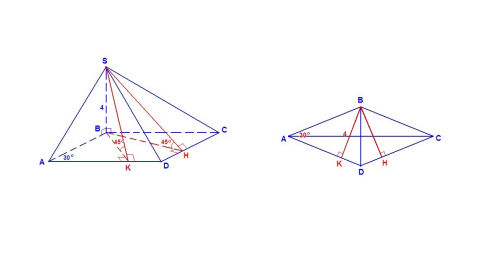
Пусть ребро SB⊥(АВС). SB - высота пирамиды. Тогда
(SAB)⊥(ABC) и (SBC)⊥(ABC)
Если ребро SB перпендикулярно основанию, то оно перпендикулярно каждой прямой, лежащей в основании:
SB⊥AB, SB⊥BC, значит ∠АВС = 150° - линейный угол двугранного угла между гранями SAB и SBC.
Тогда ∠BAD в ромбе равен 30° (так как сумма углов, прилежащих к одной стороне ромба, равна 180°).
Проведем ВК⊥AD и ВН⊥CD. ВK и ВH - проекции наклонных SK и SH на плоскость основания, значит
SK⊥AD, SH⊥CD по теореме о трех перпендикулярах.
Тогда ∠SKB = ∠SHB = 45° - линейные углы двугранных углов наклона двух других боковых граней к плоскости основания.
SB = 4 см.
Так как треугольники SBK и SBH прямоугольные, равнобедренные, то ВК = ВН = SB = 4 см, а SK = SH = 4√2 см (как гипотенузы равнобедренных треугольников).
ΔАВК: (∠ВКА = 90°) ВК = 4 см, ∠А = 30°, тогда АВ = 2ВК = 8 см (по свойству катета, лежащего напротив угла в 30°).
Ssba = Ssbc = 1/2 · AB · SB = 1/2 · 8 · 4 = 16 см²
Ssad = Sscd = 1/2 · AD · SK = 1/2 · 8 · 4√2 = 16√2 см²
Sбок = Ssba + Ssbc + Ssad + Sscd = 2 · 16 + 2 · 16√2 = 32(1 + √2) см²
ответ: х=0,42
Решение: 0,7(5х-1)-0,2(2х+3). Умножим 0,7 на первые скобки и -0,2 на вторые.0,7(5х-1)-0,2(2х+3)=3,5х-0,7-0,4х-0,6=0. Если нужно найти Х, то числа с Х переносим влево, а числа
без Х вправо(меняя знаки на противоположные для "свободных" чисел) . 3,5х-0,4х=0,7+0,6
3,1х=1,3
х=1,3/3,1
х=0,42