F(x)=-x³-3x²+4
f(x)=-3x²-6x
a может вернуть два корня только проходя в точках экстремум.
-3x²-6x=0
-3x(x+2)=0
x=0
x=-2
F(0)=4
F(-2)=0
a=-2 и 4 вернёт два корня.
Синус острого угла α прямоугольного треугольника – это отношение противолежащего катета к гипотенузе.
Обозначается так: sin α.
Косинус острого угла α прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
Обозначается так: cos α.

Тангенс острого угла α – это отношение противолежащего катета к прилежащему катету.
Обозначается так: tg α.
Котангенс острого угла α – это отношение прилежащего катета к противолежащему.
Обозначается так: ctg α.
Синус, косинус, тангенс и котангенс угла зависят только от величины угла.
Правила:
Катет b, противолежащий углу α, равен произведению гипотенузы на sin α:
b = c · sin α
Катет a, прилежащий к углу α, равен произведению гипотенузы на cos α:
a = c · cos α
Катет b, противоположный углу α, равен произведению второго катета на tg α:
b = a · tg α
Катет a, прилежащий к углу α, равен произведению второго катета на ctg α:
a = b · ctg α
Основные тригонометрические тождества в прямоугольном треугольнике:
(α – острый угол, противолежащий катету b и прилежащий к катету a. Сторона с – гипотенуза. β – второй острый угол).
b
sin α = —
c
sin2 α + cos2 α = 1
α + β = 90˚
a
cos α = —
c
1
1 + tg2 α = ——
cos2 α
cos α = sin β
b
tg α = —
a
1
1 + ctg2 α = ——
sin2 α
sin α = cos β
a
ctg α = —
b
1 1
1 + —— = ——
tg2 α sin2 α
tg α = ctg β
sin α
tg α = ——
cos α
При возрастании острого угла sin α и tg α возрастают, а cos α убывает.
Для любого острого угла α:
sin (90° – α) = cos α
cos (90° – α) = sin α
Пример-пояснение:
Пусть в прямоугольном треугольнике АВС
АВ = 6,
ВС = 3,
угол А = 30º.
Выясним синус угла А и косинус угла В.

Решение.
1) Сначала находим величину угла В. Тут все так как в прямоугольном треугольнике сумма острых углов равна 90º, то угол В = 60º:
В = 90º – 30º = 60º.
2) Вычислим sin A. Мы знаем, что синус равен отношению противолежащего катета к гипотенузе. Для угла А противолежащим катетом является сторона ВС. Итак:
BC 3 1
sin A = —— = — = —
AB 6 2
3) Теперь вычислим cos B. Мы знаем, что косинус равен отношению прилежащего катета к гипотенузе. Для угла В прилежащим катетом является все та же сторона ВС. Это значит, что нам снова надо разделить ВС на АВ – то есть совершить те же действия, что и при вычислении синуса угла А:
BC 3 1
cos B = —— = — = —
AB 6 2
В итоге получается:
sin A = cos B = 1/2.
Или:
sin 30º = cos 60º = 1/2.
Из этого следует, что в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла – и наоборот. Именно это и означают наши две формулы:
sin (90° – α) = cos α
cos (90° – α) = sin α
Убедимся в этом еще раз:
1) Пусть α = 60º. Подставив значение α в формулу синуса, получим:
sin (90º – 60º) = cos 60º.
sin 30º = cos 60º.
2) Пусть α = 30º. Подставив значение α в формулу косинуса, получим:
cos (90° – 30º) = sin 30º.
cos 60° = sin 30º.
(Подробнее о тригонометрии - см.раздел Алгебра)
Главная
Физика
Химия
Алгебра
Геометрия
История России
Русский язык
Литература
Таблицы
Тесты (проверь себя)
Полезные
В своем детстве Алеша сталкивается со многими людьми, и хорошими, и плохими. Но есть среди них человек, которому принадлежит особая роль. Это бабушка Акулина Ивановна. Бабушка всегда остается в центре его внимания, являясь посредником между мальчиком и большим миром, от нее Алеша получает самые ценные жизненные уроки. Бабушка – самый добрый человек среди Кашириных. Ее отличает бескорыстная любовь к миру, жалость к людям, чуткость к чужой обиде и боли. Она всем старается поддержать, ухаживает за больными, лечит детей, разбирает семейные споры и ссоры. Точную характеристику ей дает мастер Григорий: «Она вроде святой, хоть и вино пьет, табак нюхает. Блаженная как бы». Бабушка Акулина Ивановна оказала огромное влияние на формирование характера Алеши, его восприятие окружающего мира, отношение к людям. Переняв ее жизненную стойкость, он готов начать новую, самостоятельную жизнь. Благодарность бабушке выражена в словах Алеши: «…Это ее бескорыстная любовь к миру обогатила меня, насытив крепкой
2) Несомненно, важнейшим человеком в жизни Алеши Пешкова – главного героя повести – стала его бабушка. Впервые мальчик увидел ее после смерти отца – она приехала забирать их с мамой «на житье» к деду. Тогда бабушка показалась Алеше «черной, мягкой и удивительно интересной» . А еще странной – все ее слова и манеры были непривычны для мальчика. Но очень скоро Алеша подружился с бабушкой – настолько добрым, ласковым и веселым человеком она была.
Именно бабушка познакомила мальчика с русским фольклором – слушать сказки из ее уст было истинным удовольствием: «Говорит, точно поет, и чем дальше, тем складней звучат слова. Слушать ее невыразимо приятно» . И именно бабушка привила внуку любовь к слову - яркому, сочному, меткому.
В доме у деда, где Алеша чувствовал себя неспокойно и неуютно, единственной заступницей его была бабушка. Конечно, окончательное решение всегда оставалось за дедом как за главой семьи, но она изо всех сил пыталась оградить внука от того, что происходило в доме. А там шла непрекращающаяся война – между дедом и его детьми. И лишь бабушка пыталась как-то сохранить семью, пыталась напомнить всем этим людям, что они родная кровь.
Для Алеши Пешкова бабушка стала тем светом, который должен быть у каждого в жизни. Она стала самым верным его другом, "самым понятным и близким человеком". "Вся она — темная, но светилась изнутри.. . неугасимым, веселым и теплым светом".
Бескорыстной любви учился Алеша именно у бабушки, так как дедова семья, куда он невольно попал, жила по суровым правилам, установленным дедом-узурпатором.
Бабушка заменила Алеше мать, которая вскоре после переезда в дом отца, «исчезла» . Эта старая женщина стала тем лучиком света, который поддерживал маленького мальчика, дарил ему радость жизни, тепло и любовь в каждодневной борьбе за существование. Она пыталась внука от дедушкиного гнева, когда тот чуть не засек Алешу до смерти, всегда была на его стороне, всегда поддерживала и оберегала.
Именно бабушка открыла Алеше Бога – не сурового и злого, как у Кашириных, а доброго, снисходительного, любящего. Именно бабушка учила мальчика жизни, объясняя ему все, что происходит вокруг, в доме и за его пределами. И так продолжалось до самой ее смерти. А когда бабушка умерла, закончилось и детство героя - он пошел «в люди» .
Бабушка заменила ему мать, осветила его жизнь любовью, прорастила в нем его талант: «До нее как будто спал я, спрятанный в темноте, но явилась она, разбудила, вывела на свет, связала всё вокруг меня в непрерывную нить, сплела всё в разноцветное кружево и сразу стала на всю жизнь другом, самым близким сердцу моему, самым понятным и дорогим человеком, — это ее бескорыстная любовь к миру обогатила меня, насытив крепкой силой для трудной жизни».
Подробнее - на -
1) Дана функция y= -x^3-3x^2+4.
Её производная равна y' = -3x² - 6x = -3x(x + 2).
Приравняем её нулю: -3x(x + 2) = 0. Находим 2 критические точки:
х = 0 и х = -2.
Определяем их свойства по изменению знака производной.
х = -3 -2 -1 0 1
y' = -9 0 3 0 -9 .
В точке х = -2 минимум функции, у = 0.
В точке х = 0 максимум, у = 4.
На промежутках (-∞; -2) и (0; +∞) функция убывает
на промежутке (-2; 0) возрастает.
Вторая производная равна y'' = -6x - 6 = -6(x + 1).
Отсюда определяем точку перегиба х = -1.
х = -2 -1 0
y'' = 6 0 -6.
График выпуклый: (-1; +∞), вогнутый (-∞; -1).
Пересечение с осями решается алгебраически:
- с осью Оу при х = 0 у = 4.
- с осью Ох при у = 0 надо решить кубическое уравнение
-x^3-3x^2+4 = 0. Один корень виден: х = 1.
Делим -x³ - 3x² + 4 | х - 1
-x³ + x² -x² - 4x - 4
-4x² + 4
-4x² + 4x
-4x + 4
-4x + 4.
Результат -(x² + 4x + 4) = -(х + 2)².
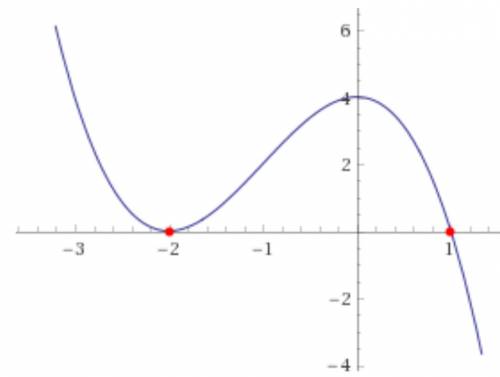
Получили 2 точки пересечения: х = 1 и х = -2.
График приведен в приложении.
2) Возможные случаи состава корней кубического уравнения исчерпываются тремя, описанными ниже. Эти случаи легко различаются с дискриминанта
Δ = -4b³d + b²c² - 4ac³ + 18abcd - 27a²d².
Итак, возможны только три случая:
Если Δ > 0, тогда уравнение имеет три различных вещественных корня.
Если Δ < 0, то уравнение имеет один вещественный и пару комплексно сопряжённых корней.
Если Δ = 0, тогда хотя бы два корня совпадают.
Рассмотрим уравнение -x^3-3x^2+4=0.
Его коэффициенты a b c d
-1 -3 0 4
Определяем дискриминант:
-4b^3*d b^2*c^2 -4a*c^3 18abcd -27*a^2*d^2 Дискрим
инант
432 0 0 0 -432 0.
Как видим, при а = 0 уравнение имеет 2 корня.
Это видно и по графику.