

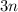 - где n число. Подставим к примеру три натуральных числа вместо n. И получим нужные нам числа:
- где n число. Подставим к примеру три натуральных числа вместо n. И получим нужные нам числа:
 - где m число. Подставим к примеру три натуральных числа вместо m. И получим нужные нам числа:
- где m число. Подставим к примеру три натуральных числа вместо m. И получим нужные нам числа: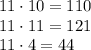
ответ: а) нет решения б) 3,63; -3,7
Пошаговое объяснение:
а) модуль не может быть отрицательны, поэтому здесь нет решения
ответ: нет решения
б) |15x+0.5|=55
15x+0.5=55 15x+0.5=-55
15x=54.5 15x=-55.5
x=3.63 x=-3.7
ответ: 3,63; -3,7