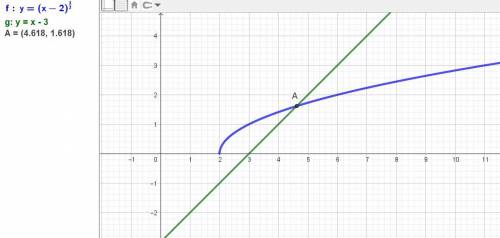
Дано уравнение: √(x - 2) = x - 3.
ОДЗ: х - 2 > 0, x > 2.
Надо обе части уравнения возвести в квадрат.
х - 2 = х² - 6х + 9.
Получаем квадратное уравнение:
х² - 7x + 11 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-7)^2-4*1*11=49-4*11=49-44=5;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√5-(-7))/(2*1)=(√5+7)/2=√5/2+7/2=√5/2+3.5~~4.618034;
x_2=(-√5-(-7))/(2*1)=(-√5+7)/2=-√5/2+7/2=-√5/2+3.5~~2.381966.
Получили 2 корня - это результат лишнего корня при возведении в квадрат, но должна быть одна точка пересечения одной ветви параболы и прямой.
Второй корень не подходит.
ответ: х1 = √5/2+3,5.
Пошаговое объяснение:
y = [ ( x²+ 1 )( x - 2 )]/( 2 - x ) = - ( x²+ 1 ) = - x² - 1 ;
Отже , дана функція дорівнює функції у = - х² - 1 без точки ( 2 ;- 5 ) .
Спочатку рисуємо параболу у = - х² , далі переносимо паралельно
вздовж осі Оу вниз на 1 . На одержаній кривій "виколюємо "
точку ( 2 ; - 5 ) .
Визначимо , при яких k пряма y = kx має з побудованим графіком одну
спільну точку . Рішаємо систему рівнянь :
{ у = - х² - 1 ,
{ y = kx ; ⇒ kx = - x² - 1 ;
x² + kx + 1 = 0 ;
D = k² - 4 ; D = 0 ; k² - 4 = 0 ; k² = 4 ; k = ± 2 .
При k = - 2 і при k = 2 буде одна спільна точка .
1) (x+4)^2 = 3x+40
x^2+8x+16-3x+40=0
x1 = -8
x2 = 3
2) 2.5-0.4*3 =
=  *
* = 7
= 7
3) 2205 и 2475
Наибольший общий делитель::
Разложим числа на простые множители и подчеркнем общие множители чисел:
2205 = 3 · 3 · 5 · 7 · 7
2475 = 3 · 3 · 5 · 5 · 11
Общие множители чисел: 3; 3; 5
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД (2205; 2475) = 3 · 3 · 5 = 45
4)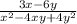 =
=  =
= 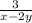
5) y-5>4y+4
y<-3
(-∞;-3)