1. х³ - х² + х - 1 = х³ - х² + х - 1
2. х³ + х² - х - 1 = х³ + х² - х - 1
3. х² + 2(a + b)x + 4ab = х² +2(a + b)x + 4ab
4. х² - 7х + 12 = х² - 7х + 12
Пошаговое объяснение:
Доказать тождество - это значит показать, что его обе части равны, т.е. его левая часть тождественно равна правой части для любых допустимых значений переменных.
1. х³ - х² + х - 1 = (х - 1)(х² + 1) - преобразуем выражение в правой части и получим выражение в левой части:
(х - 1)(х² + 1) = х*х² - 1*х² + х*1 - 1*1 = х³ - х² + х - 1 - получили одинаковые выражения в левой и правой частях:
х³ - х² + х - 1 = х³ - х² + х - 1
2. х³ + х² - х - 1 = (х² - 1)(х + 1) - преобразуем выражение в правой части и получим выражение в левой части:
(х² - 1)(х + 1) = х²*х - 1*х + х²*1 - 1*1 = х³ - х + х² - 1 = х³ + х² - х - 1 получили одинаковые выражения в левой и правой частях:
х³ + х² - х - 1 = х³ + х² - х - 1
3. (х + 2а)(х + 2b) = х² +2(a + b)x + 4ab - преобразуем выражение в левой части и получим выражение в правой части:
(х + 2а)(х + 2b) = х² + 2ах + 2bх + 4аb = х² + 2(а + b)х + 4аb - получили одинаковые выражения в левой и правой частях:
х² + 2(a + b)x + 4ab = х² +2(a + b)x + 4ab
4. (х - 15)(х + 8) + 132 = (х - 3)(х - 4) - преобразуем оба выражения в левой и правой частях и получим равные выражения в правой и левой частях:
(х - 15)(х + 8) + 132 = х² - 15х + 8х - 120 + 132 = х² - 7х + 12 - левая часть
(х - 3)(х - 4) = х² - 3х - 4х + 12 = х² - 7х + 12 - правая часть
получили одинаковые выражения в левой и правой частях:
х² - 7х + 12 = х² - 7х + 12
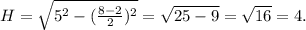
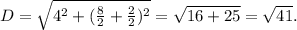
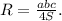
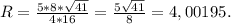
ответ:оуопуутудиуоцьцид
Пошаговое объяснение: