Видимо, 21 город в некотором государстве, а не в школе.
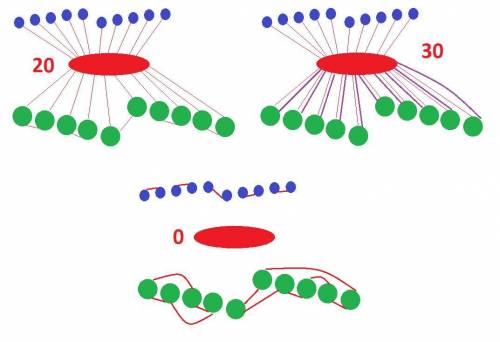
Каждая дорога имеет 2 конца. В 10 малых городах 10 концов дорог, в 10 средних городах 20 концов дорог. Всего 20 + 10 = 30 концов дорог.
Из столицы может выходить любое чётное количество дорог от 0 до 30 при условии, что нет дорог, которые начинаются и заканчиваются в столице.
Например, если каждый малый и средний город соединены со столицей, а средние города по парам между собой, то из столицы будет выходить 20 дорог.
Например, каждый город связан со столицей по воздуху (самолёты), а все дороги построены между малыми и средними городами. Тогда из столицы не выходит ни одной дороги.
Например, каждый малый город связан со столицей одной дорогой, а каждый средний город связан со столицей двумя дорогами разного назначения. Тогда из столицы выходит 30 дорог.
ответ : 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30
25. Уравнением параболы у=ах²+bx+c, если парабола пересекает ось ОХ, то у=0, а точки пересечения находят, решая уравнение ах²+bx+c=0, уравнение третьего ответа не имеет корней, т.е. если у=0, то в уравнение у=х²+2 вместо у ставим нуль, и х²=-2, чего быть не может. Значит, эта парабола не пересекает ось ОХ, у первого, второго и четвертого дискриминант больше нуля, значит, есть корни и точки пересечения, а последний ответ не является уравнением параболы.
ответ. у =х²+2
29. Первое не может быть целым,т.к. если числа простые, то они и взаимно простые, значит, не имеют общих делителей, кроме единицы.
Второе равенство не может быть верным, т.к. если х²у²=х²⇒х²(у²-1)=0, у=±1 или х=0, ни одно из этих чисел не является простым.
третье может быть верным, если у=2, х=3, 2³/4=2
четвертое не может быть верным, т.к. единственным четным числом простым является два, если его умножить на любое нечетное простое, и сократить на два, четного целого не получим.
Чтобы выполнялось пятое, надо чтобы основания были равны, т.е. х=у, но тогда они не будут простыми, т.к. все простые различны по условию.
ответ уˣ/4- четное целое.
а-6 =4-6 × А=-2÷А=8
Пошаговое объяснение:
нужно отнять и потом умнодить