90, 630
Пошаговое объяснение:
НОД(А, 100) = 10. 100 = 2²·5², 10 = 2·5. НОД — это минимальные степени общих простых множителей среди двух чисел. Так как 2 и 5 в НОД содержатся только в первой степени, а в числе 100 — во второй, А = 2·5·...
НОК(А, 84) = 1260. 1260 = 2²·3²·5·7, 84 = 2²·3·7. НОК — это максимальные степени простых множителей среди двух чисел. Так как 84 содержит 3 только в первой степени, а НОК — во второй, А = 2·3²·5·... При этом число А не должно содержать простых множителей, отличных от тех, что есть в НОК. Число 1260 и 84 содержат 7 в первой степени, поэтому А может как её содержать, так и не содержать. Значит, существует два варианта числа А: 2·3²·5 = 90 и 2·3²·5·7 = 630.
3) A(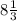 ) B(7.5) C(
) B(7.5) C(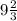 ) D(
) D(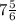 ) E(
) E(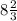 ) F(
) F(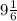 )
)
Середина DF (8.5)
4) A(0.3) B(1.5) C(0.8) D(1.2) E(2) F(3)
Середина DF (2.1)
Пошаговое объяснение:
3) Считаем количество черточек между 8 и 10. Их 12.
Одна черточка соответствует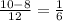
(·) А находится на 2-ой от 8, значит ее координата: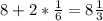
(·) B находится на 3-ей назад от 8, значит ее координата: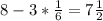
Аналогично для всех остальных точек
Середина DF: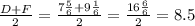
4) Считаем количество черточек между 0 и 1. Их 10.
Одна черточка соответствует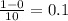
(·) А находится на 3-ей от 0, значит ее координата: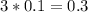
(·) B находится на 5-ой от 1, значит ее координата: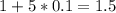
Аналогично для всех остальных точек
Середина DF: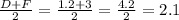
============
Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!