Пошаговое объяснение:
1. 3001
2. 1600*2=3200
3. 4
4. 800+56= 856
5. 6000-200=5980
6. 430 - 170= 260
260\10=26
7.320*1/4=80
8.3000
9.4500-500=4000
10. 30-20=10 - ширина участка
30*10=300
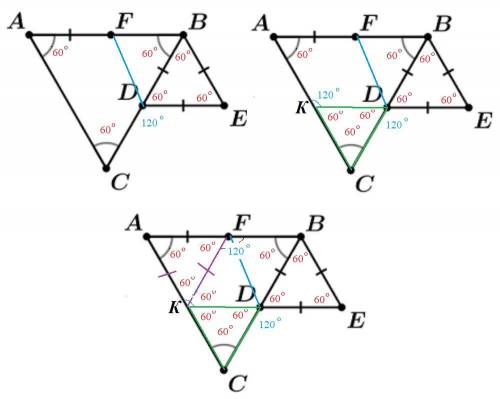
Δ АВС - равностороний ( все углы равны ∠А=∠В=∠С=60°) ⇒
АВ=ВС=АС
Δ DBE - равностороний ( все стороны равны DB=BE=DE) ⇒
∠ DBE=∠BED=∠EDB=60°
AB || DE так как внутренние накрест лежащие углы равны
∠ ABD =∠BDE=60°
∠CDE=180°-∠BDE=180°-60°=120°⇒∠CDE+∠CAD=180°
Продолжим DE до пересечения с АС в точке К
В четырехугольнике АВЕК
∠ АКЕ=360°-∠САВ-∠АВE-BED=360°-60°-(60°+60°)-60°=120°
Четырехугольник АВЕК - параллелограмм, противоположные углы равны.
⇒ BE=AK
По условию BE=AF ⇒ AK=AF и Δ AKF - равнобедренный,
с углом при вершине 60°
Значит, Δ AKF - равносторонний.
KF=AF=BE
KFBE - равнобедренная трапеция
∠ FKD=60°
∠BFK=120°
Четырехугольник KFBD - параллелограмм, противоположные углы равны.
FB=KD
FK=BD
и тогда FB=KD
О т в е т. ∠CDE+∠CAD=180°
Δ АВС - равностороний ( все углы равны ∠А=∠В=∠С=60°) ⇒
АВ=ВС=АС
Δ DBE - равностороний ( все стороны равны DB=BE=DE) ⇒
∠ DBE=∠BED=∠EDB=60°
AB || DE так как внутренние накрест лежащие углы равны
∠ ABD =∠BDE=60°
∠CDE=180°-∠BDE=180°-60°=120°⇒∠CDE+∠CAD=180°
Продолжим DE до пересечения с АС в точке К
В четырехугольнике АВЕК
∠ АКЕ=360°-∠САВ-∠АВE-BED=360°-60°-(60°+60°)-60°=120°
Четырехугольник АВЕК - параллелограмм, противоположные углы равны.
⇒ BE=AK
По условию BE=AF ⇒ AK=AF и Δ AKF - равнобедренный,
с углом при вершине 60°
Значит, Δ AKF - равносторонний.
KF=AF=BE
KFBE - равнобедренная трапеция
∠ FKD=60°
∠BFK=120°
Четырехугольник KFBD - параллелограмм, противоположные углы равны.
FB=KD
FK=BD
и тогда FB=KD
О т в е т. ∠CDE+∠CAD=180°

ответ: 1) 2999
2) 3200
3) 2400
4) 8056
5) 5980
6) 60
7) 80
8) 3000
9) 4000
10) 300