Через 4 часа моторная лодка встретится с плотом после выхода из пункта B.
Пошаговое объяснение:
Требуется найти, через какое время моторная лодка встретится с плотом после выхода из пункта B.
Плот проплывает расстояние между пунктами A и B за 20 часов. Такое же расстояние моторная лодка проплывает по озеру за 5 часов.
Вспомним формулы:
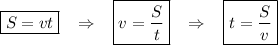
1. Пусть расстояние от А до В - S км.
Тогда скорость плота - Vтеч. =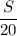 
км/ч.
Заметим, что скорость плота равна скорости течения.
Собственная скорость лодки - Vл =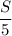 
км/ч.
⇒
Скорость лодки по течению:
Vпо теч. = Vл+Vтеч. =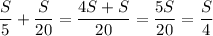 
(км/ч)
Скорость лодки против течения:
Vпр.теч. = Vл - Vтеч. =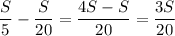 
(км/ч)
2. Рассмотрим движения из пункта А в пункт В.
Скорость плота - 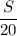км/ч; скорость лодки по течению - 
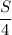км/ч
⇒ скорость лодки по течению в 5 раз больше, чем скорость плота.
То есть, когда лодка приплывет в пункт В, плот проплывет 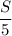км и будет находиться в М.
3. Когда плот оказался в точке М, лодка развернулась и поплыла против течения со скоростью -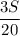 
км/ч.
Теперь можем считать, что одновременно навстречу друг другу выплыли плот и лодка соответственно из М и В, расстояние между которыми
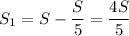(км)
Найдем искомое время до их встречи.
Для этого найдем скорость сближения:
Vc = Vп + Vпр.теч. =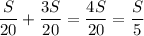 
(км/ч)
4. Зная расстояние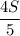 
км и скорость 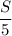км/ч, мы можем найти искомое время:
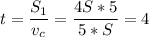(ч).
Через 4 часа моторная лодка встретится с плотом после выхода из пункта B.
m=-0,5, m=2,5
Пошаговое объяснение:
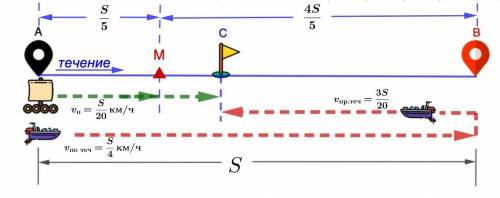
График кусочно-линейной функции (см. рисунок)
состоит из двух лучей и отрезка.
y=m - это прямая, параллельная оси Ох. Поэтому:
а) при m<-0,5 прямая y=m пересекает только луч прямой y=3·x-3,5, то есть только одна общая точка;
б) при -0,5<m<2,5 прямая y=m пересекает луч прямой y=3·x-3,5, отрезок прямой y=-3·x+8,5 и луч прямой y=3,5·x-11, то есть три общих точек;
в) при m>2,5 прямая y=m пересекает только луч прямой y=3,5·x-11, то есть только одна общая точка.
ответом будут (заштрихованные прямые) только : m= -0,5 и m =2,5.