Пошаговое объяснение:
№1
1-2/9=9/9-2/9=7/9 (осталось выполнить)
№2
70/105 (Сокращаем на 5)=14/21 (Сокращаем на 7)=1/3
№3
1/7+3/4 (домножаем для общего знаменателя 28)=4/28+21/28=25/28
№4
 =1114*(-35)/4=-38990/4 (сокращаем на 2)=-19495/2=-9747
=1114*(-35)/4=-38990/4 (сокращаем на 2)=-19495/2=-9747 =-9747,5
=-9747,5
№5
7/25*5=35/25 (сокращаем на 5)=7/5=1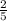 =1,4
=1,4
№6
9/28:18/35=(9*35)/(28*18) сокращаем 9 и 18 (делим на 9)=35/56=5/8
№7
5/6*х=4(1/2)
х=4(1/2)/(5/6)
х=27/5=5,4
№8
7/8*7/8=49/64
№9
5/7*35=25 (см)
№10
4(5/11)*22/98=49/11*22/98 (сокращаем (49 и 98) и (11 и 22))=2/2=1
№11
60/2*5=150
№12
Всего 68 га
Первый день 68*1/4=17 га
Второй день (68-17)*2/3=34 га
Третий день 68-17-34=17 га
№13
(7/12+11/30х):7/14=1/3
(7/12+11/30х)*14/7=1/3
22/30х=1/3-14/12
22/30х=-5/6
х=-25/22=-1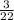
Відповідь:
Покрокове пояснення:
2.
х делит у
Отношение
Рефлексивное х:х
Транзитивное, х:у & у:с→ х:с
Тождественное х:у & у:х → х=у
Не симетричное, отношение порядка
х≠у
Транзитивное, х≠у & у≠с→ х≠с
Симетричное х≠у → у≠х
Антирефлексивное х≠х есть ложь
Количество лет х соврадает с возрастом у
Так как понятия лет и возраст єквивалентни, то отношение есть
Симетричное, тождественное, рефоексивное, транзитивное → єквивалентно
3.
Рефлексивние:
Бит знакомим, бить не више, иметь тех же родителей
Симметрични:
Бить знакомим, иметь тех же родителей
Транзитивни
Бить старше или бить младше, бить више, иметь тех же родителей, бить братом
1.
Третье множество рефлексивно, симметрично, транзитивно. Отношение еквивалентности
Первое отношение - антисиметричное
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, общим решением которого является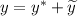 .
.
1)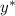 — общее решение соответствующего линейного однородного дифференциального уравнения:
— общее решение соответствующего линейного однородного дифференциального уравнения:
Применим метод Эйлера: сделаем замену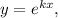 где
где 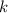 — некоторая постоянная. Тогда
— некоторая постоянная. Тогда 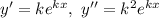
Получили характеристическое уравнение:
Разделим обе части уравнения на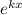 :
:
Отрицательный дискриминант означает, что корни данного уравнения будут комплексно-сопряженными:
Тогда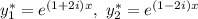
Воспользуемся формулой Эйлера: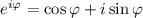
Фундаментальная система решений: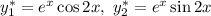 — функции линейно независимые, поскольку
— функции линейно независимые, поскольку 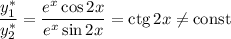
Общее решение: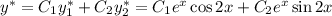
2)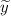 — частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции
— частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции 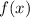 .
.
Здесь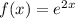 , причем
, причем 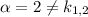 , поэтому частное решение имеет вид
, поэтому частное решение имеет вид 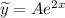 , где
, где 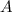 — неизвестный коэффициент, который нужно найти.
— неизвестный коэффициент, который нужно найти.
Тогда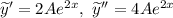 и
и 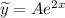 подставим в исходное ЛНДР и найдем
подставим в исходное ЛНДР и найдем 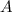 :
:
Разделим обе части уравнения на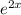
Таким образом, частное решение: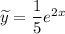
Тогда общим решением исходного ЛНДР с постоянными коэффициентами:
ответ: