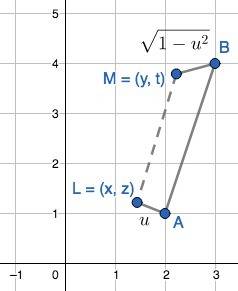
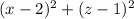 – квадрат длины отрезка AL,
– квадрат длины отрезка AL, 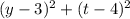 – квадрат длины отрезка BM,
– квадрат длины отрезка BM, 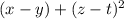 – квадрат длины отрезка LM.
– квадрат длины отрезка LM. 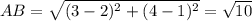 . Поскольку по условию
. Поскольку по условию 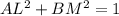 , то AL, BM < 1, и минимальное значение LM (а значит, и
, то AL, BM < 1, и минимальное значение LM (а значит, и  ) будет достигаться тогда, когда L и M лежат на отрезке AB.
) будет достигаться тогда, когда L и M лежат на отрезке AB.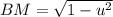 , AL + BM = v.
, AL + BM = v. 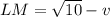 будет минимально, когда v (и
будет минимально, когда v (и 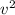 ) будет максимально.
) будет максимально.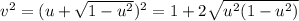
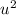 , его максимум достигается в вершине, когда
, его максимум достигается в вершине, когда 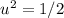 , при этом
, при этом 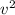 достигает максимального значения 2, поэтому максимальное значение v равно
достигает максимального значения 2, поэтому максимальное значение v равно 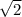
 равно:
равно: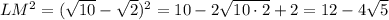
суму найменшого одноцифрового числа і найбільшого троцифрового зменш у 100 разів
(1+999):100=10