Надеюсь я Если эта информация вам отметить мой ответ "лучшим"
Пошаговое объяснение:
Отец>Сын - 4 раза.
Сын<Отец - на 35.
Возьмём Сына за х, Отец тогда 4х.
Пусть Отец будет у, Сын тогда y-35.
{x=y-35.
{y=4x.
{x-4x=-35.
{y=4x.
Решим уравнение x-4x=-35.
-3x=-35.
x=11⅔, то есть сыну 11 лет и 8 месяцев.
Если сын младше на 35 лет, то соответственно Отец старше на 35.
11 лет и 8 месяцев+35 лет = 46 лет и 8 месяцев.
Сыну 11 лет и 8 месяцев.
Отцу 46 лет и 8 месяцев.
1)
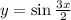 ; Синус - это периодическая функция.
; Синус - это периодическая функция.
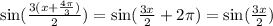 ; Поэтому у данной функции есть период. Просмотрим остальные:
; Поэтому у данной функции есть период. Просмотрим остальные:
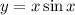 ; Пусть у этой функции есть период T:
; Пусть у этой функции есть период T: 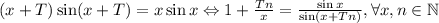 ; Выберем такое число x и n, что выполняются следующие условия:
; Выберем такое число x и n, что выполняются следующие условия: 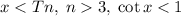 ; Тогда левая часть будет больше правой, что невозможно.
; Тогда левая часть будет больше правой, что невозможно.
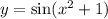 ; Пусть функция имеет период T:
; Пусть функция имеет период T:
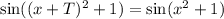
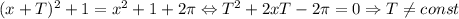 ; Получили противоречие.
; Получили противоречие.
С оставшимися аналогично.
ответ: А;
2) 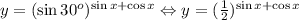 ; Функция монотонно убывает по мере роста показателя степени.
; Функция монотонно убывает по мере роста показателя степени.
Заметим, что 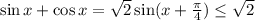 ; Значит,
; Значит,  ;
;
3) 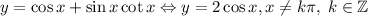 ; С этими условиями область значений равна [-2;2]; Если брать в расчет все значения x, то придется выколоть все точки с ординатами 2 или -2; Получаем, что E(f)=(-2;2);
; С этими условиями область значений равна [-2;2]; Если брать в расчет все значения x, то придется выколоть все точки с ординатами 2 или -2; Получаем, что E(f)=(-2;2);
4) Пусть sin A - первый корень какого-нибудь квадратного трехчлена, а -cos A - его второй корень. Тогда квадратное уравнение примет такой один из возможных видов: 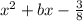 ;
;
В итоге, получаем: 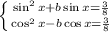 ; Сложим два уравнения:
; Сложим два уравнения:
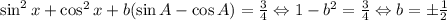 ;
;
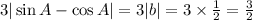
1)
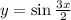 ; Синус - это периодическая функция.
; Синус - это периодическая функция.
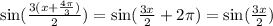 ; Поэтому у данной функции есть период. Просмотрим остальные:
; Поэтому у данной функции есть период. Просмотрим остальные:
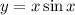 ; Пусть у этой функции есть период T:
; Пусть у этой функции есть период T: 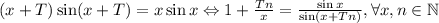 ; Выберем такое число x и n, что выполняются следующие условия:
; Выберем такое число x и n, что выполняются следующие условия: 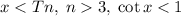 ; Тогда левая часть будет больше правой, что невозможно.
; Тогда левая часть будет больше правой, что невозможно.
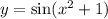 ; Пусть функция имеет период T:
; Пусть функция имеет период T:
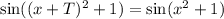
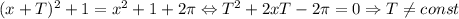 ; Получили противоречие.
; Получили противоречие.
С оставшимися аналогично.
ответ: А;
2) 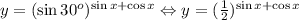 ; Функция монотонно убывает по мере роста показателя степени.
; Функция монотонно убывает по мере роста показателя степени.
Заметим, что 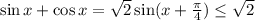 ; Значит,
; Значит,  ;
;
3) 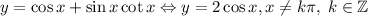 ; С этими условиями область значений равна [-2;2]; Если брать в расчет все значения x, то придется выколоть все точки с ординатами 2 или -2; Получаем, что E(f)=(-2;2);
; С этими условиями область значений равна [-2;2]; Если брать в расчет все значения x, то придется выколоть все точки с ординатами 2 или -2; Получаем, что E(f)=(-2;2);
4) Пусть sin A - первый корень какого-нибудь квадратного трехчлена, а -cos A - его второй корень. Тогда квадратное уравнение примет такой один из возможных видов: 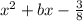 ;
;
В итоге, получаем: 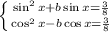 ; Сложим два уравнения:
; Сложим два уравнения:
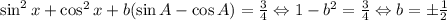 ;
;
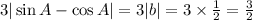
Пошаговое объяснение:
вот ответ на твой вопрос