отмена крепостного права в 1861 году имело неоднозначное значение для россии. с одной стороны, крестьяне, много лет проведшие в неволе рады были освобождению из рабства, с другой стороны не знали как жить дальше. они не видели другой жизни, вне границ поместья, у них не было домов, собственных участков земли. обрезки, выделяемые государством были неплодородны, малы по размерам, поэтому бывшим крепостным не хватало сил, для возделывание этих участков. итак, я считаю, что отмена крепостного права 1861 года было не самым лучшим решением, даже для самих же крестьян.
Пошаговое объяснение:
перепишем уравнение заданной прямой в виде y = kx+b
2y+x +3 = 0
y = -0.5x -1.5
отсюда мы найдем коэффициент наклона нашей нормали. т.к. нормаль должна быть ║ заданной прямой, то и угловые коэффициенты у них должны быть равными.
т.о. угловой коэффициент наклона нормали = -0,5
уравнение нормали
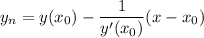
теперь надо найти точку кривой, в которой
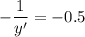

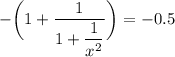
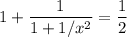
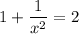
отсюда получим х = ± 1
т.е. у нас есть две точки с абсциссами х=1 и х = -1, принадлежащие кривой у= х -1/х, удовлетворяющие нашим условиям построения нормали
две точки потому, что график функции у = х -1/х состоит из двух кривых
теперь для нормали в виде у = kx+b у нас есть x. найдем у и b
у(1) = 0 0=-0,5*1+b b= 0.5
уравнение нормали у = -0,5х +0,5
у(-1) = 0 0= -0,5*(-1)+b b = -0.5
уравнение нормали у = -0,5х -0,5
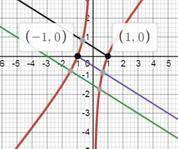
на графике
красным у = х -1/х
зеленым 2у+х+3 = 0
фиолетовым и зеленым - две нормали. специально их укоротила, чтобы было видно к какой дуге кривой относится каждая нормаль
Відповідь:
1) x⁴-8x²+7=0
x^4-8x^2+7=0
x^2=a
a^2+8a+7=0
D=64-7*4=64-28=36=6^2
a1/2=-7;-1
x^2=-1 x^2=-7
x1=1
x2=49
2) (x²-5x+2)(x²-5x-1)=28
Заміна: x²-5x=a
(a+2)(a-1)=28
a²+a-2-28=0
a²+a-30=0
a₁=5; a₂=-6 (корені знайдені по т. Вієта)
x²-5x=5 x²-5x=-6
x²-5x-5=0 x²-5x+6=0
D=(-5)²-4*1*(-5)=45 x₃=2; x₄=3 (корені знайдені по т. Вієта)
x₁=(5+√45)/2
x₂=(5-√45)/2
x₁*x₂*x₃*x₄=((5+√45)/2)*((5-√45)/2)*2*3 = ((25-45)/4)*6=(-20/4)*6=-5*6=-30
3)3x-5/x²-1=3x+2/x²+x -6x-5/x²-x
Тільки 2)