Задача имеет два решения.
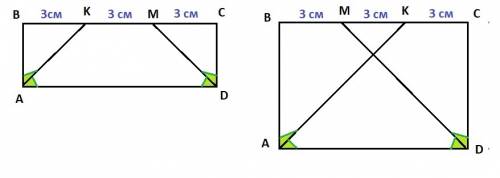
1) Прямоугольник ABCD : AK и DM - биссектрисы; BK = KM = MC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = 3 см
BC = BK + KM + MC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (3 + 9) · 2 = 24 см
P = 24 см
================================
2) Прямоугольник ABCD : AK и DM - биссектрисы; BM = MK = KC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = BM + MK = 3 + 3 = 6 см
BC = BM + MK + KC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (6 + 9) · 2 = 30 см
P = 30 см
Пошаговое объяснение:
Сторони паралелограма дорівнюють 4.4 см і 5.6 см. Висота проведена до більшої сторони, дорівнює 3,3 см. Обчисліть другу висоту цього паралелограма. Дуже Дякую.
Нехай сторона а = 5.8 см, b = 4.4 см, h_a = 3 см. Знайти h_b.
Знайдемо площу паралелограма:
S = a\cdot h_a\\S = 5.8\cdot 3 = 17.4 \:\: (cm^2)
Використавши формулу ще раз, знайдемо другу висоту:
S = b\cdot h_b \:\Rightarrow \:h_b = \frac{S}{b} \\h_b = \frac{17.4}{4.4} = 3.9 \:\: (cm)
Відповідь: Друга висота паралелограма рівна 3.9 см.