1.чтобы сложить два числа с одинаковыми знаками надо поставить их общий знак и приписать модулей. примеры:(-3) + (-6) = -(3 + 6) = -9; (+3) + (+5) = +(3 + 5) = +8 2. Чтобы сложить два числа с разными знаками и разными модулями нужно поставить знак числа большего приписать к нему разность меньшего. примеры: -2+1 = -1; 5+ (-3)=2. 3. Сумма противоположных чисел равна нулю. примеры:-2+2=0; -8+8=0. 4. Если одно из слагаемых равно нулю то сумма равна второму слагаемому. примеры: 0+2=2; 22+0=22 Приведите по два примера на каждое правило
Рівняння вигляду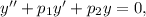 де
де 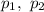 — задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
— задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
Метод Ейлера (метод характеристичних рівнянь) дозволяє знаходити загальний розв'язок для вказаного рівняння.
Розв'язок цього рівняння шукаємо у вигляді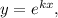 де
де 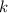 — деяка стала (дійсна чи комплексна). Тоді, якщо
— деяка стала (дійсна чи комплексна). Тоді, якщо 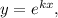 то
то 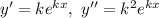
Можливі три випадки:
➀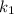 і
і 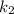 — дійсні,
— дійсні, 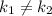
Фундаментальна система розв'язків: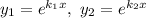 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 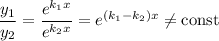
Загальний розв'язок: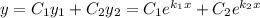
Приклад: а)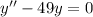
Метод Ейлера: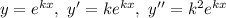
Характеристичне рівняння: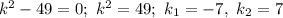
Загальний розв'язок: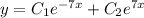
Відповідь: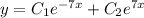
Приклад: в)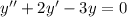
Метод Ейлера: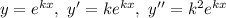
Характеристичне рівняння: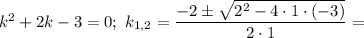
Загальний розв'язок: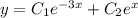
Відповідь: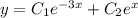
➁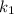 і
і 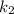 — дійсні,
— дійсні, 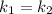
Якщо покласти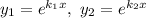 , то ці функції лінійно залежні, бо
, то ці функції лінійно залежні, бо 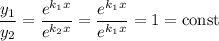
Фундаментальна система розв'язків: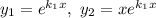 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 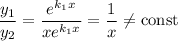
Загальний розв'язок: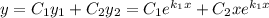
➂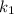 і
і 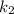 — комплексно спряжені,
— комплексно спряжені, 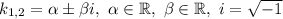
Фундаментальна система розв'язків: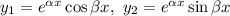 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 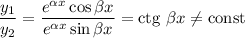
Загальний розв'язок: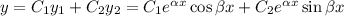
Приклад: б)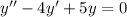
Метод Ейлера: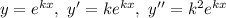
Характеристичне рівняння: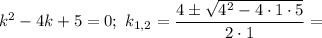
Отже,
Загальний розв'язок: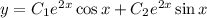
Відповідь: