Число 9,72 (является или не является) решением неравенства |t|≤9,72.

👇

Увидеть ответ

Ответ:

99880

01.03.2023

ответ: да, является

Пошаговое объяснение:

-9,72≤t≤9,72

9,72 входит в эту область

4,8(42 оценок)

Ответ:

Gay1122

01.03.2023

Да

Решением неравенства с переменной называют значение переменной, которое обращает неравенство с переменной в верное числовое неравенство.

Если подставить вместо t 9,72, то будет правильно. Там же больше или равно.

4,5(27 оценок)

Открыть все ответы

Ответ:

денис1095

01.03.2023

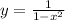
Исследовать функцию и построить график $y = \frac{1}{1- x^{2}}$

1) Область определения функции
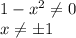
$1- x^{2} \neq 0 \\ x \neq \pm 1$

2) Точки пересечения графика функции с осью OY
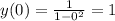$y (0) = \frac{1}{1- 0^{2}} = 1$ точка пересечение (0; 1)

3) Исследуем функции на четность

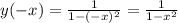
$y(-x) = \frac{1}{1- (-x)^{2}} = \frac{1}{1- x^{2}}$

Так как 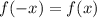f(-x) = f(x) , то функция является четной

4) Функция имеет две точки разрыва -1 и 1 , поэтому график функции имеет две вертикальные асимптоты х =-1 и х =1.

Найдем наклонные асимптоты y = k*x + b , где

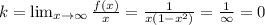
$k = \lim_{x \to \infty} \frac{f(x)}{x} = \frac{1}{x(1-x^2)} = \frac{1}{ \infty} = 0$

Так как k=0, то наклонных асимптот нет, а есть горизонтальные.

Найдем теперь коэффициент b.

$b= \lim_{x \to \infty} [f(x)-kx] = \frac{1}{1- x^{2}} = \frac{1}{ \infty} = 0$

Подставляем найденные коэффициенты в формулу y = kx + b, получаем, что y = 0 - горизонтальная асимптота.

5) Найдем экстремумы функции. Для это найдем производную y' и приравняем ее к нулю y' = 0

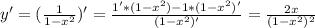
$y' = (\frac{1}{1- x^{2}})' = \frac{1' * (1- x^{2} ) - 1*(1-x^2)'}{(1- x^{2} )'} = \frac{2x}{(1-x^2)^2}$

Тогда

$\frac{2x}{(1-x^2)^2} = 0 \ \Rightarrow \ x =0$

Получилась одна критическая точка.

6) Найденные точки разрыва и точки экстремума, разбивают область определения на четыре интервала. Находим знак производной (у') на каждом интервале.

x x<-1 -1<x<0 0 0<x<1 x>1

y' - - 0 + +

y убыв. убыв. 1 воз. воз.

В точке экстремума (х=0) производная меняет знак с "-" на "+" значит это точка минимума.

7) Найдем точки перегиба и промежутки выпуклости и вогнутости. Для этого найдем вторую производную

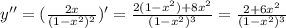
$y'' = ( \frac{2x}{(1- x^{2} )^2} )' = \frac{2(1- x^{2} )+8 x^{2} }{(1- x^{2} )^3} = \frac{2+6 x^{2} }{(1- x^{2} )^3}$

Решаем методом интервалов

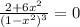
$\frac{2+6 x^{2} }{(1- x^{2} )^3} =0$

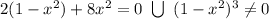
$2(1- x^{2} )+8 x^{2} = 0 \ \bigcup \ }{(1- x^{2} )^3 \neq 0$

Корней нет, значит точек перегиба нет и 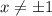$x \neq \pm1$

Отмечаем на числовой прямой все найденные точки разрыва и критические точки , в нашем случае это точки –1; 0 ; 1.

Методом интервалов определяем знаки 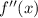f''(x) на полученных интервалах.

Интервал X < -1 ,

f''(x) = "–" < 0 - график функции является выпуклым на данном интервале;

Интервал – 1 < X < 1 ,

f''(x) = "+" > 0 - график функции является вогнутым на данном интервале;

Интервал X > 1 ,

f''(x) = "–" < 0 - график функции является выпуклым на данном интервале;

8) Построим график функции. Данные для построения и сам график, представлены ниже

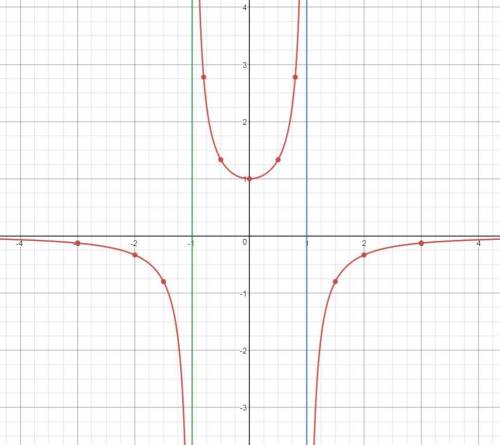
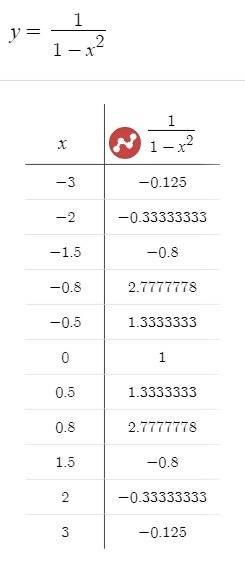
Y=1/1-x^2 исследовать функцию и построить график

4,7(22 оценок)

Ответ:

шрщорзо

01.03.2023

1)Du schreibst höflich; du erhältst eine höfliche Antwort.
Je höflicher er schreibt,eine desto höflichere Antwort erhält er.
2)Du triffst ihn oft; du wirst mit ihm ein gutes Verhältnis haben.
Je öfter du ihn triffst,ein desto besseres Verhältnis wirst du mit ihm haben.
3)Du willst schnell fahren; du musst einen teuren Wagen kaufen.
Je schneller du fahren willst,einen desto teuereren Wagen du kaufen musst.
4)Das Geld ist knapp; du musst einen hohen Zinssatz zahlen.
Je knappar das Geld ist,einen desto höheren Zinssatz du zahlen musst.
5)Wir kamen dem Ziel nah; ein starkes Hungergefühl quälte mich.
Je näher wir dem Ziel kamen,ein desto stärkeres Hungergefühl quälte mich.

4,4(30 оценок)

Это интересно:

Взаимоотношения

23.05.2020

Хитрость как искусство: Как стать хорошим лжецом...

Компьютеры-и-электроника

05.11.2022

Хочешь создать свою банду в GTA San Andreas? Просто следуй этим шагам!...

Стиль-и-уход-за-собой

14.02.2023

Контроль волос африканского стиля: советы и инструкции...

Философия-и-религия