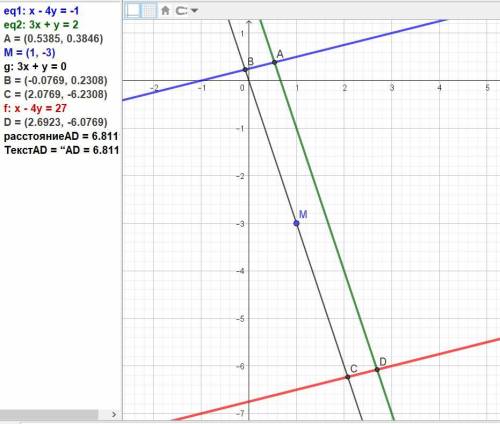
Уравнение прямой, включающей сторону ВС, найдём, подставив координаты точки М в уравнение с координатами переменных, как у параллельной прямой AD 3x + y – 2 = 0.
3*1 + (-3) + C = 0, отсюда С = -3 + 3 = 0.
Получаем уравнение BC: 3x + y = 0.
Находим вершину B параллелограмма как точку пересечения прямых АВ и ВС, решив систему:
{x – 4y + 1 = 0 x – 4y + 1 = 0
{3x + y = 0 (x4) = 12x + 4y = 0
13x + 1 = 0, x = -1/13,
y = – 3x = – 3(-1/13) = 3/13. Точка В((-1/13); (3/13)).
Находим точку С как симметричную точке В относительно точки М(1; -3).
х(С) = 2х(М) – х(В) = 2*1 - (-1/13) = 27/13,
y(С) = 2y(М) – y(В) = 2*(-3) - (3/13) = -81/13.
Уравнение прямой, включающей сторону CD, найдём, подставив координаты точки C в уравнение с координатами переменных, как у параллельной прямой AB x - 4y + 1 = 0.
(27/13) - 4(-81/13) + C = 0, отсюда С = (-27/13) – (324/13) = -351/13 = -27.
Получаем уравнение CD: x - 4y - 27 = 0.
находим первый ? в первой строке - (164-156)/2 = 4, ? = 156+4 = 160
первая строка выглядит так - 156-160-164
находим первый ? во второй строке - (156-152)/2 = 2, ? = 156-2 = 154
вторая строка выглядит так - 154-158-?
находим второй ? во второй строке (158-154) = 4, ? = 158+4 = 162
вторая строка выглядит так - 154-158-162
строки теперь выглядят так:
156-160-164
154-158-162
152-? -?
находим первый ? в третей строке (160-158) = 2, ? 158-2 = 156
третья строка теперь выглядит так - 152-156-?
находим второй ? в третей строке (156-152) = 4, ? = 156+4 = 160
третья строка теперь выглядит так: 152-156-160
теперь все соединяем:
156-160-164
154-158-162
152-156-160
теперь все делим на 2 и наверное получаем волшебный квадрат:
78-80-82
77-79-81
76-78-80
"волшебство" скорее всего в том, что каждый следующий столбик (с низу в верх) начинается с того числа, которым заканчивается предыдущий столбик)))