х ≤ 5 часов
Пошаговое объяснение:
"Сколько времени может гореть ... чтобы от неё осталось не менее одной трети." Не менее! То есть не обязательно что б она горела до момента пока не останеться 1/3, может остаться и больше.
Найдем крайнее значение до которого может сгореть свеча (2/3):
30 ×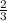 
= 20 см
Составим пропорцию:
1 час горения - 4 см свечи
Х часов горения - 20 см свечи
Х = 20 / 4 = 5 часов
Если свеча будет гореть (допустим!) 4 часа, то останеться не менее 1/3 от свечи. Если же свеча будет гореть больше чем 5 часов то останеться меньше 1/3 от свечи. Значит ответом на вопрос задачи будет, что свеча должна гореть не больше 5 часов или же:
х ≤ 5 часов
Пошаговое объяснение:
355.
Т. к. ΔАВС -прямоугольный, то по теореме Пифагора
АВ^2=AC^2+BC^2 ⇒ AB^2=108+36=144. AB=√144=12. BC=√36=6
sinA=BC/AB=6/12=1/2. ⇒ ∠A=30°, a ∠B=90°-30°=60°
354.
Пусть меньший катет треугольника х см, а гипотенуза-у см. Т. к. 1-н из острых углов 60°, то 2-й - 90°-60°=30°. Но в прямоугольном Δ-ке катет,лежащий против угла в 30° равен половине гипотенузы. Следовательно у=2х. Согласно условию составим уравнение
х*у=128 или х*2х=128. 2х^2=128. x^2=64. x=√64=8 см - меньший катет, а 8*2=16 см - гипотенуза.
А)3×8=24м²
Б) (3+8)×2=22м
В) 1)2,5×3-1,5=6
2)7,5-2,1=5,4
3)(2,5×8)×2=40
4)6+5,4+40=51,4