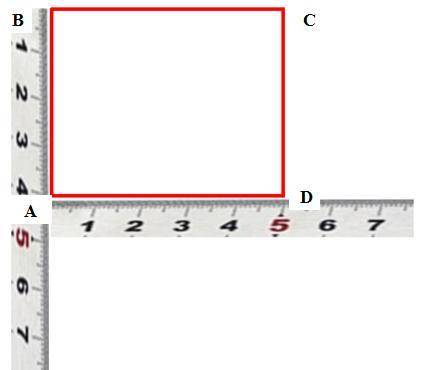
С линейки построим и обозначим вершины через ABCD (см. рисунок 1).
1. Вычислим периметр прямоугольник со сторонами AB=4 см и AD=5 см по формуле периметра:
P=2·(AB + AD)=2·(4 см + 5 см)= 2·9 см= 18 см
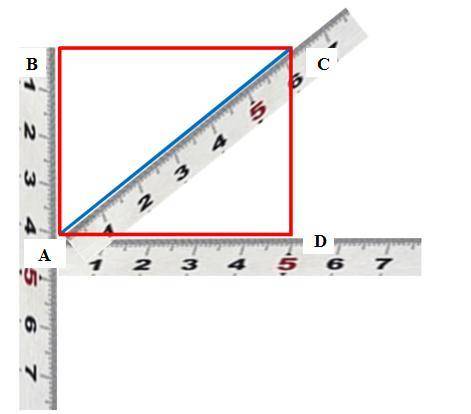
2. Проведем диагональ AC прямоугольника и измерим её (см. рисунок 2). Длина AC равна приблизительно 6,4 см. Тогда, так как 5 < 6,4, то большая сторона прямоугольника AD < AC.
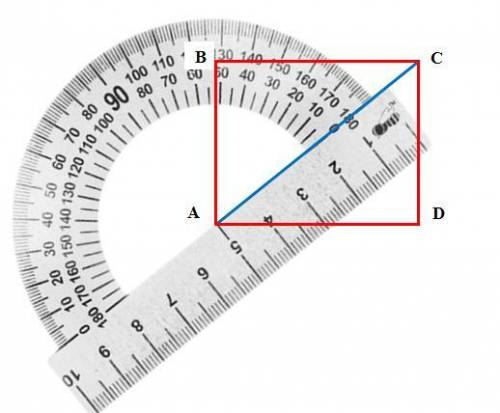
3. С транспортира измерим угол между диагональю и меньшей стороной прямоугольника (см. рисунок 3). Угол составляет приблизительно 52°.
27413:x+319=398
1) х находится в знаменателе дроби. Перенесем его в числитель.
Для это необходимо умножить правую и левую часть уравнения на х.
В итоге получим: 27413+319х=398х
2) Перенесем неизвестные слагаемые в левую часть, а известные в правую. Напоминаю,что при переносе слагаемого из одной части уравнения в другую, знак слагаемого изменяется.
В итоге: 319х-398х=-27413
Умножим все уравнение на минус единицу. Получим:
-319х+398х=27413
79х=27413
х=27413:79
х=347
ответ: х=347