Задание 1.
во вложениях
Задание 2.
Пусть 3х - яблонь в саду, тогда х - груш.
По условию задачи, когда вырубили 14 яблонь и посадили 10 груш, деревьев стало поровну.
Составим и решим уравнение:
3х - 14 = х + 10
3х - х = 10 + 14
2х = 24
х = 12 - количество груш в саду
Т. к. по условию задачи яблонь в 3 раза больше, чем груш, то:
12 × 3 = 36 - количество яблонь в саду
ответ: 12 груш и 36 яблонь.
Задание 3.
а) 3( х + 0,6) = 3 - х
3х + 1,8 = 3 - х
3х + х = 3 - 1,8
4х = 1,2
х = 0,3
ответ: 0,3.
б) во вложениях
Задание 4.
2,5 : 8,75 = х : 21
х = 2,5 × 21 ÷ 8,75
х = 6
ответ: 6.
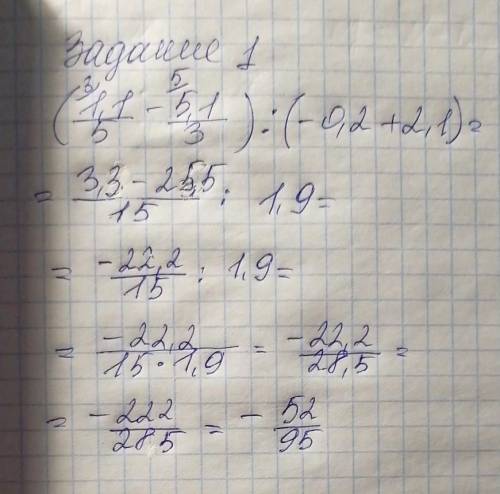

НОД (100; 300) = 100.
НОК (100, 300) = 300
Пошаговое объяснение:
НОК
Разложим на простые множители 100
100 = 2 • 2 • 5 • 5
Разложим на простые множители 300
300 = 2 • 2 • 3 • 5 • 5
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 5 , 5
Находим произведение одинаковых простых множителей и записываем ответ
НОД (100; 300) = 2 • 2 • 5 • 5 = 100
НОД
Разложим на простые множители 100
100 = 2 • 2 • 5 • 5
Разложим на простые множители 300
300 = 2 • 2 • 3 • 5 • 5
Выберем в разложении меньшего числа (100) множители, которые не вошли в разложение
Все множители меньшего числа входят в состав большего
Добавим эти множители в разложение бóльшего числа
2 , 2 , 3 , 5 , 5
Полученное произведение запишем в ответ.
НОК (100, 300) = 2 • 2 • 3 • 5 • 5 = 300
Пошаговое объяснение:
Правильный ответ: 2)