Отметим точки E и F прямоугольника EGHF на стороне AC, а точку G и H на сторонах AB и BC соответственно. Пересечение высоты BD и отрезка GH отметим через D1.
Обозначим GH через x.
Т.к. в прямоугольнике EGHF сторона GH параллельна стороне EF, которая лежит на стороне AC треугольника ABC, то GH || AC, а следовательно ΔGBH≈ΔABC
Тогда
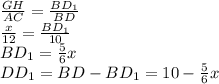
Отметим, что GE = DD1 и найдем площадь прямоугольника EGHF:
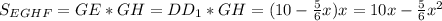
Т.е. нам надо найти максимум функции 
Для этого найдем ее производную и приравняем 0:
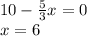
Значит x = 6 является точкой максимума функции.
Значение функции в точке максимума: 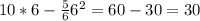
ответ: наибольшее значение площади такого прямоугольника 30 см2
12у+18=0 или 1,6-0,2у=0
у=-18/12 у=-1,6/-0,2
у=-1,5 у=8
ответ: у=-1,5 или у=8
Пошаговое объяснение: