а) а = 24 = (2*2*2) * 3; b = 56 = (2*2*2) * 7; С = 3 * 7 = 21
НОК (a;b) = (2*2*2) * 3 * 7 = 168 - наименьшее общее кратное
НОД (a;b) = (2*2*2) = 8 - наибольший общий делитель
НОК : НОД = 168 : 8 = 21 = С
б) а = 264 = (2*2*2) * 3 * 11; b = 582 = 2 * 3 * 97; С = (2*2) * 11 * 97 = 4268
НОК (a;b) = (2*2*2) * 3 * 11 * 97 = 25608 - наименьшее общее кратное
НОД (a;b) = 2 * 3 = 6 - наибольший общий делитель
НОК : НОД = 25608 : 6 = 4268 = С
в) а = 22 = 2 * 11; b = 176 = (2*2*2*2) * 11; С = (2*2*2) = 8
НОК (a;b) = (2*2*2*2) * 11 = 176 - наименьшее общее кратное
НОД (a;b) = 2 * 11 = 22 - наибольший общий делитель
НОК : НОД = 176 : 22 = 8 = С
г) а = 68 = (2*2) * 17; b = 256 = (2*2*2*2*2*2*2*2); С = (2*2*2*2*2*2) * 17 = 1088
НОК (a;b) = (2*2*2*2*2*2*2*2) * 17 = 4352 - наименьшее общее кратное
НОД (a;b) = (2*2) = 4 - наибольший общий делитель
НОК : НОД = 4352 : 4 = 1088 = С
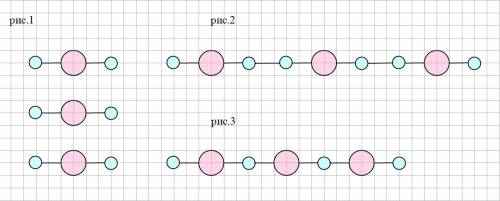
Если взрослые идут отдельно (рис. 1), например, первый взрослый с двумя детьми, за ним - второй, за ним - третий, то детей будет в 2 раза больше, чем взрослых, а взрослых, соответственно, в 2 раза меньше, чем детей.
Если все идут в одну шеренгу, то возможны два варианта:
1). (рис. 2) между тремя взрослыми 2 по 2 ребенка и по одному - с краев шеренги. В этом случае детей также будет в 2 раза больше (6), чем взрослых (3), а взрослых - в 2 раза меньше, чем детей.
2). (рис. 3) между тремя взрослыми 2 по 1 ребенку и по одному - с краев шеренги. В этом случае детей будет 4, а взрослых - 3. И взрослых будет в 1 1/3 раза меньше, чем детей, однако условие задачи будет соблюдено. То есть каждый взрослый ведет за руку двоих детей..))
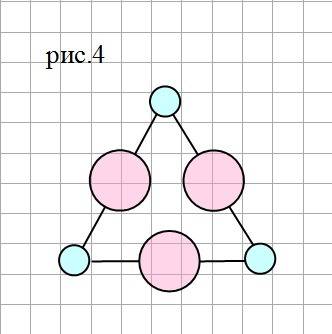
Ну, и совсем уже невероятный вариант - на рис.4..)) - В этом случае детей и взрослых одинаково: 3 и 3, но каждый взрослый ведет за руку двоих детей..)))