Во всех примерах используем формулу площади круга
Sкр = πR².
1.
На рисунке закрашена 1/6 часть круга.
Радиус круга - 4 клеточки, значит величина радиуса
R = 4 · 0.5 см = 2 см
Площадь закрашенной фигуры:
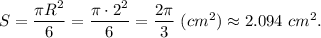
2. На рисунке изображены:
1 - верхняя половина большого круга радиуса 4 клеточки или
R = 2 cм;
2 - Из половины большого круга вырезана половина маленького круга радиуса 2 клеточки или r = 1 см;
3 - Снизу добавлена половина маленького круга радиуса 2 клеточки или r = 1 см.
Поскольку площадь выреза равна площади нижней половины маленького круга, то в результате площадь закрашенной фигуры равна площади половины большого круга:
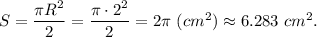
3. На рисунке изображен квадрат со стороной а = 8 клеточек или
а = 4 см.
Из квадрата вырезаны две половины круга радиуса 4 клеточки или
R = 2 cм. Таким образом вырезан целый круг.
Площадь закрашенной фигуры равна
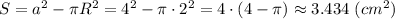
а)12аb-5а-ab-6а=11ab-11а
б) 15х³-10х²-20х
2.вынесем общий множитель за скобки
3х²+9ху=3х(х+3у)
10х∧5-5х=5х(2х∧4-1)
3.раскроем скобки и решим уравнение
4х+4=15х-14х-35
4х-15х+14х=-35-4
3х=-39
х=-13
4. пусть х дет делает ученик, мастер делает х+6
8х=5(х+6)
8х=5х+30
8х-5х=30
3х=30
х=10 дет в час делает ученик
10+6=16 дет мастер
5. наименьший общий знаменатель 12. домножим
8х-4х-2=9х-15
4х-9х=-15+2
-5х=-13
х=13/5=7,5
6) раскроем скобки
4ха+4х²+4ху+4а²-4ах-4ау-4ух+4уа+4у²=4х²+4а²+4у²