До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
ответ:
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
Учитывая, что угол находится в первой четверти,
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
создаются и эксплуатируются системы контроля за химической обстановкой в районах химически опасных объектов и локальные системы оповещения о химической опасности; разрабатываются планы действий по предупреждению и ликвидации последствий химической аварии; накапливаются, хранятся и поддерживаются в готовности средства индивидуальной защиты органов дыхания и кожи, приборы химической разведки, дегазирующие вещества; поддерживаются в готовности к использованию убежища, обеспечивающие защиту людей от АХОВ; принимаются меры по защите продовольствия, пи-щевого сырья, фуража, источников (запасов) воды от загрязнения АХОВ; проводится подготовка населения к действиям в условиях химических аварий, подготовка аварийно подразделений и персонала химически опасных объектов; обеспечивается готовность сил и средств подсистем и звеньев РСЧС, на территориях которых находятся химически опасные объекты, к ликвидации последствий химических аварий.<br />Основными мероприятиями химической защиты, осуществляемыми в случае возникновения химической аварии, являются: обнаружение факта химической аварии и оповещение о ней; выявление химической обстановки в зоне химической аварии; соблюдение режимов поведения на территории, заражённой АХОВ, норм и правил химической безопасности; обеспечение населения, персонала аварийного объекта, участников ликвидации последствий химической аварии средствами индивидуальной защиты органов дыхания и кожи, применение этих средств; эвакуация населения, при необходимости, из зоны аварии и зон возможного химического загрязнения; укрытие населения и персонала в убежищах, обеспечивающих защиту от АХОВ; оперативное применение антидотов и средств обработки кожных покровов; санитарная обработка населения, персонала аварийного объекта, участников ликвидации последствий аварии; дегазация аварийного объекта, объектов производственного, социального, жилого назначения, территории, технических средств, средств защиты, одежды и другого имущества
7.
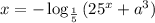
Пусть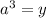
, количество корней от этого не изменится.
Рассмотрим функцию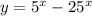
:
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно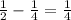
. Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
ответ:![(0; \frac{\sqrt[3]{2}}{2})](/tpl/images/0445/7312/80965.png)
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
Учитывая, что угол находится в первой четверти,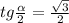
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
Решая аналогичное уравнение, получаем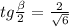
ответ: 4 : 3