Номер 1463 решите системы уравнений по этому образцу
образец
{(2х-3у=4 │•(7),7х-5у=25 ⃓∙(-2) )┤
+{(14х-21у=28,@-14х+10у=-50;@)┤
-11у= -22
у = -22 :(-11)
у=2
Подставив это значение у в первое уравнение системы 2х-3у=4, получим
2х-3∙2=4
2х -6= 4
2х= 4+6
2х= 10
х= 10:2
х=5
Проверка {(2•5-3•2=4, 7•5-5•2=25;)┤ (4=4,25=25.)┤
ответ (5;2)
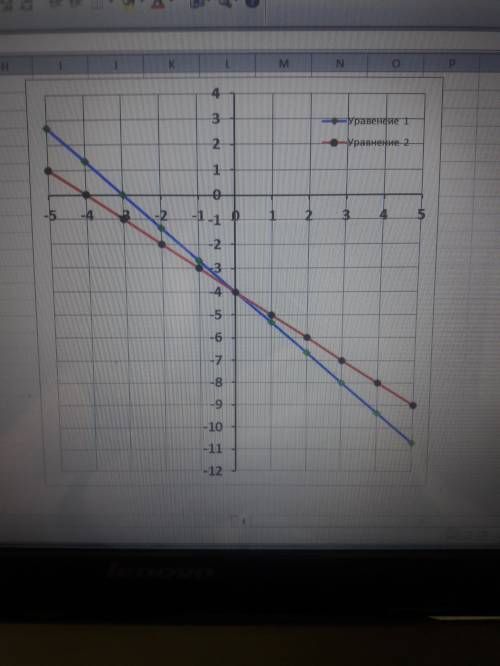
2) Определяем эти точки для каждого уравнения, для этого сначала принимаем х=0, затем у=0.
Для первого уравнения:
При х = 0 4*0 + 3у = -12
3у = -12
у = -4 значит первая точка имеет координаты (0; -4)
При у=0 4х + 3*0 + -12
4х = -12
х = -3 Значит вторая точка имеет координаты (-3; 0)
Аналогично проводим такие же вычисления для второго уравнения и находим точки с координатами: (0; -4) и (-4; 0)
3) Проводим две прямые через точки и точка пересечения этих прямых и есть решение системы уравнений.
Смотрите приложениею
ответ: х = 0 ; у = -4