Пошаговое объяснение:
для удобства построения графика функции приведем ее в привычный вид квадратичной функции. выделим полный квадрат
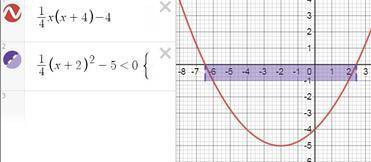
0,25х(x+4)-4 = 0
0.25(x² +4x -16) = 0.25(x² +4x +4-20) = 0.25(x+2)²-5
теперь легко построить график
у = 0.25(x+2)²-5
строим у = х², расширяем ветви на 0,25, смещаем график на -2 по оси ох (на 2 влево) и на -5 по оси оу (на 5 вниз.)
теперь определяем точки по оси х, где график <0
целые решения попадают в интервал [-6; 2]
осталось посчитать модули
|-6| + |-5| + |-4| + |-3| + |-2| + |-1| + 0 + |1| + |2| = 24
x^2+1 = -x+3; x^2+x-2 = 0; x1 = -2; x2 = 1.
Шаг 2: Находим определенный интеграл функции y = -x+3 в пределах от -2 до 1.
Первообразная этой функции будет Y = -1/2*x^2 + 3x + С
Подставляя пределы интегрирования получаем площадь под функцией S1 = -1/2 + 3 + 2 + 6 = 10,5.
Шаг 3: Находим определенный интеграл функции y = x^2+1 в пределах от -2 до 1.
Первообразная этой функции будет Y = 1/3*x^3 + x + С
Подставляя пределы интегрирования получаем площадь под функцией S2 = 1/3 + 1 + 8/3 +2 = 6.