Пошаговое объяснение:
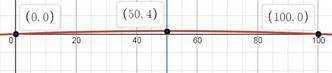
график будет такой
у = -0,0016(х-50)²+4
сместим систему координат так, чтобы центр находиля в вершине параболы (т.е. перенос по х на 50 вправо, по у на -4 (на 4 вверх))
в этой системе нарисуем "базовый" график у = -х² и увидим, что
при х = 50 у= -2500,
а нам надо 4, значит мы должны "расширить" параболу на
4/(-2500) = -0,0016 - это коэффициент а, т.е. мы уже получили часть искомого уравнения, выглядит так
у = -0,0016х²
дальше просто вернем систему координат "на родину",
т.е. на 50 влево по х и поднимем вверх на 4
и получим график
у = -0,0016(х-50)² + 4
это не хрестоматийный решения графика по точкам, классически надо брать общее уравнение у= ах² + bx + c, подставлять туда поочередно координаты трех точек и получить систему трех уравнений с тремя неизвестными а потом эту систему решать......
а строить путем смещения системы координат и быстрее и приятнее...
график полученной функции у = -0,0016(х-50)² + 4 я проверила. он удовлетворяет заданным условиям
V=πR²H/3. V1- объем конуса ДО изменений
V2- объем конуса ПОСЛЕ изменений
1. h=H/2 r=2R
V2=πr²h/3
V2=4πR²H/6=2πR²H/3- объем конуса после изменений
V1/V2=πR²H/3 : 2πR²H/3
V1/V2=1/2
V2=2V1
объем конуса после изменений увеличился в 2 раза.
2. h=H/3 r=R/3
V2=πr²h/3
V2=π(R/3)²(H/3)/3= πR²H/81 - объем конуса после изменений
V1/V2=πR²H/3 : πR²H/81 = 81/2
V1/V2=27
V2=V1/27
объем конуса уменьшился в 27раз