1. Метод исключения неизвестных.
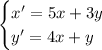
Продифференцируем первое уравнение:
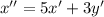
Подставим выражение для y':
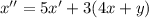
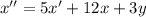
Из получившегося уравнения отнимем первое уравнение системы:
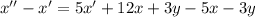
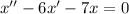
Составим характеристическое уравнение:
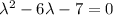
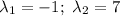
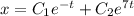
Найдем производную:
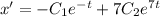
Выразим из первого уравнение системы у:
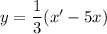
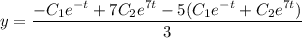
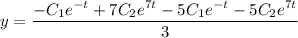
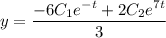
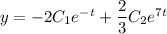
Общее решение:
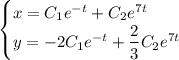
Находим решение задачи Коши:
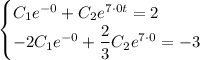
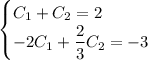
Первое уравнение домножим на 2:
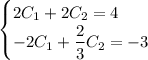
Сложим уравнения:
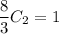
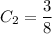
Выразим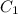 
:
Частное решение:
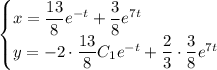
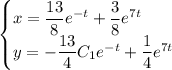
2. Метод характеристических уравнений (метод Эйлера).
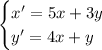
Матрица из коэффициентов при неизвестных:
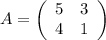
Характеристическая матрица:
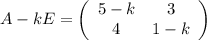
Характеристическое уравнение:
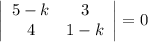
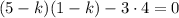
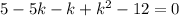
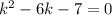
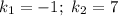
Общее решение:
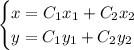
Ищем фундаментальную систему решений:
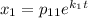
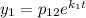
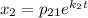
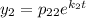
Для нахождения чисел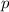 
составим систему:
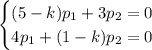
Для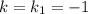 
:
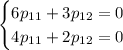
Оба уравнения дают:
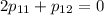
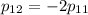
Найдем ненулевое решение. Пусть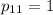 
. Тогда 
.
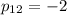Для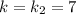 
:
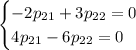
Оба уравнения дают:
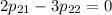
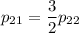
Найдем ненулевое решение. Пусть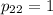 
. Тогда 
.
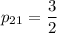Фундаментальная система решений найдена:
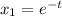
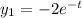
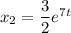
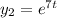
Общее решение:
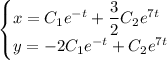
Находим частное решение:
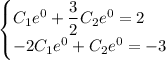
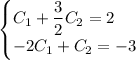
Первое уравнение домножим на 2:
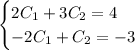
Сложим уравнения:
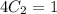
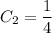
Выразим :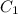
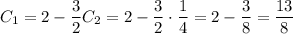
Частное решение:
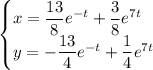
1:
1) 80 • 5=400(км) — легковая машина
2) 60•5=300(км) — грузовая машина
3) 400+300=700(км)
2:
1) (70+8)•2=156(см)
3:
Фото
4:
1) 2500 – х = 1500
x=2500-1500
х=1000
Проверка:
2500-1000=1500
1500=1500
2) 100 • х = 300 + 900
100•х=1200
х=1200:100
х=12
Проверка:
100•12=300+900
12=12
5:
40дм=4м
5кг>500г
400см<40м
6:
Если произведение означает минус, тогда 174,5!