5/9 = 5 : 9 = 0,555...
Пошаговое объяснение:
То есть в частном после запятой бесконечно повторяется 5.
В полученном частном 0,555...цифра 5 и является периодом.
Данный период записывается при скобок.
0,555... = 0,(5).
ответ: lim xn=ln2.
Пошаговое объяснение:
Так как n≠0, то выражение 2^(1/n), а вместе с ним и выражение xn=n*[2^(1/n)-1], определены при любом натуральном n. Для нахождения предела последовательности положим 1/n=m. Тогда n=1/m, при n⇒∞ m⇒0 и выражение примет вид: (2^m-1)/m. Если m⇒0, то 2^m-1⇒0 и мы имеем неопределённость вида 0/0. Для нахождения её предела используем правило Лопиталя: (2^x-1)'=(2^x)*ln2, x'=1, поэтому искомый предел равен пределу выражения (2^x-1)'/x'=(2^x)*ln2 при x⇒0. Очевидно что этот предел равен ln2.
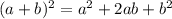упрощаем выражение в квадрате: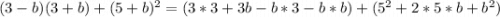
Теперь просто открываем скобки и приводим общие члены:
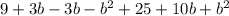- можем сократить одинаковые члены с разными знаками, например 
и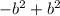 
сокращаем, потому что результат вычислений этих выражений равен 0.
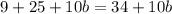- результат.
=================================
2. 
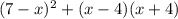
Точно также как и в первом примере, сперва первое выражение в квадрате упрощаем с формулы квадрата суммы, два вторых выражения переумножаем:
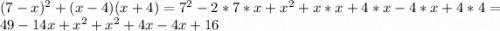
Теперь приводим общие члены, с разными знаками - "уничтожаем":
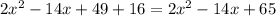
5/9=0.555...=0.(5) период равен пяти.
13/99=0.131313...=0.(13) период равен тринадцати.