1) Пусть последовательность положительных чисел
... ; 
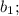
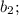
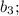
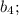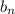
является геометрической прогрессией, тогда
с формулы общего члена геометрической прогрессии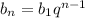 
данную последовательность представим в виде:
... ; 
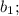
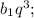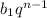
2) Прологарифмируем по основанию 
:
... ; 
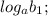
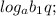
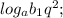
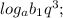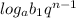
3) Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
. . . . . . . . . . . . . . . . . . . . . . . .
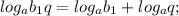
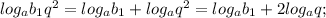
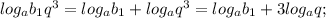
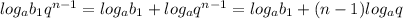
4) Рассмотрим полученную последовательность:
... ; 
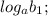
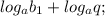
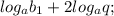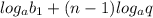
Очевидно, это арифметическая прогрессия, где
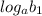- её первый член
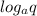- разность этой прогрессии.
Доказано.
(3-sqrt2)^2=(-6sqrt2+11)