Математика: 1. 5 212 036 – (28 175 : 35 + 403 ∙ 208 – 1 242 : 18) ∙ 7 =

1. 5 212 036 – (28 175 : 35 + 403 ∙ 208 – 1 242 : 18) ∙ 7 =

👇

Увидеть ответ

Ответ:

gavul79

29.12.2020

151026/125,1208 26/125

Пошаговое объяснение:

4,7(70 оценок)

Ответ:

vvv76

29.12.2020

4620116

Пошаговое объяснение:

5 212 036 – (28 175 : 35 + 403 ∙ 208 – 1 242 : 18) ∙ 7

1)28 175 : 35=805

2)403 ∙ 208=83824

3) 1242 : 18=69

4)805+83824-69=84560

5)84560*7=591920

6)5212036-591920=4620116

4,4(63 оценок)

Открыть все ответы

Ответ:

LoveSmile78900987

29.12.2020

Можно найти несколько пределов данной числовой последовательности. Для этого нужно посмотреть, что произойдет с ней при стремлении к бесконечности с разными знаками, и в "опасных" точках.

"Опасные" точки сразу видны, это:
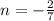1) $n=- \frac{2}{7}$ - знаменатель обращается в 0.
2) n=0

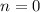- по обычаю проверяется эта точка.

Эта числовая последовательность может быть сведена ко второму замечательному пределу для нахождения пределов:
$lim (1+ \frac{1}{x})^x=e$ (при

→∞)

Выделяем целую часть в дроби:

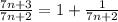
$\frac{7n+3}{7n+2 } = 1 + \frac{1}{7n+2 }$

Используем свойство 2-го замечательного предела, но добавляем степени:

$lim (1 + \frac{1}{7n+2 })^{3n-4}$

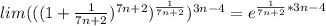$lim (((1 + \frac{1}{7n+2 })^{7n+2})^{ \frac{1}{7n+2}})^{3n-4} = e^{\frac{1}{7n+2} * 3n-4}$ (при

→∞)

То есть мы степень не меняли: домножили и разделили.

Посчитаем, что получилось:

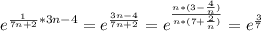$e^{\frac{1}{7n+2} * 3n-4} = e^{ \frac{3n-4}{7n+2}} = e^{ \frac{n*(3-\frac{4}{n}) }{n*(7+\frac{2}{n})} } = e^{ \frac{3}{7} }$ (при

→∞)

Итак:
1)

→+∞ предел равен $e^{ \frac{3}{7} }$
2)

→-∞ предел равен $e^{ \frac{3}{7} }$

3)

→0 предел равен:
$lim ( \frac{7n+3}{7n+2})^{3n-4} = (\frac{3}{2})^{-4} = (\frac{2}{3})^{4} = \frac{16}{81}$

4)

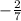
→ $- \frac{2}{7}$
По правило Лопиталя имеем: 0 (не расписывал, поскольку это очень много и неважно в данном случае, нас это не интересует).

Мы видим, что при стремлении к бесконечности с разными знаками, мы имеем конечное число. В "опасных" точках, скачков нет.

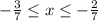Используя свойства показательной функции, находим, что график делает скачок в некотором интервале (основание должно быть неотрицательным числом, если же взять число из интервала $- \frac{3}{7} \leq x \leq - \frac{2}{7}$ - мы получаем отрицательное основание).

Можно говорить, что данная числовая последовательность является неограниченной (из-за этого интервала).

Если же этого не учитывать, то данная числовая последовательность является ограниченной (это очень грубо).

Найдите предел числовой последовательности. укажите, является ли заданная числовая последовательност

Найдите предел числовой последовательности. укажите, является ли заданная числовая последовательност

4,4(95 оценок)

Ответ:

LUCOVERUS

29.12.2020

Достижения египетской науки значительны. Была создана письменность, в математических подсчётах оперировали многозначными цифрами. В свою очередь математические навыки использовались в архитектуре, экономике, астрономии. Достаточно сказать, что египтяне имели один из самых совершенных календарей. Больших успехов достигли египтяне в медицине, чему традиция мумификации тел. Благодаря этому египтяне знали устройство человеческого тела и умели врачевать многие болезни. Значительны были познания египтян в географии. Они собирали сведения о соседних государствах, различных природных объектах, свойствах минералов и растений, имели навыки навигации. Немало знаний было накоплено и по гуманитарным наукам, особенно по истории собственной страны. Сохранились целые научные трактаты.
В Древнем Египте существенную роль играло образование. Школы существовали обычно при храмах, принимались в них только мальчики, примерно с 7 лет. В школах изучали историю, литературу, религию, географию, языки, агрономию, строительное дело, учёт и делопроизводство, астрономию, математику и медицину.

Потребности сельского хозяйства вынудили жрецов научиться вычислять разливы Нила, для чего потребовались знания астрономии. Древние египтяне пришли к необходимости составления календаря. Древнеегипетский календарь, принципы построения которого актуальны и в наши дни, разделял на 3 времени года, которые состояли из 4 месяцев каждое. В месяце было 30 дней, при этом существовало ещё 5 дней вне месяцев. Отметим, что високосные годы египтяне не использовали, поскольку их календарь опережал природный. Также египетские астрономы выделяли на небе созвездия и понимали, что они находятся на небосводе не только ночью, но и днём.

4,6(8 оценок)

Это интересно:

Здоровье

07.01.2021

Как набрать жир: эффективные способы набора массы тела...

Дом-и-сад

30.08.2022

Как освободить лезвие бритвы от ржавчины одним приемом?...

Стиль-и-уход-за-собой

25.11.2021

Обвисание груди в молодом возрасте: как избежать...

10.10.2021