√7 - ближайшие корни √4 и √9
√4 < √7 <√9
2 < √7 < 3
√7 относится к промежутку ( 2 ; 3 )
√8 - ближайшие корни √4 и √9
√4 < √8 <√9
2 < √8 < 3
√8 - относится к промежутку ( 2 ; 3 )
√48 - ближайшие корни √36 и √49
√36 < √48 <√49
6 < √48 < 7
√48 относится к промежутку ( 6 ; 7 )
√56 - ближайшие корни √49 и √64
√49 < √56 <√64
7 < √56 < 8
√56 относится к промежутку ( 7 ; 8 )
ответ: 48)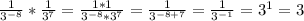
по свойству степени 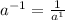
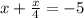 | · 4
| · 4
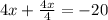
сокращаем дробь
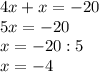
Проверка:
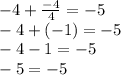
любое число в чётной степени будет положительным
-0,7 · (-10)⁴ - 8 · (-10)² - 26 =
-10⁴ = 10000
-0,7 · 10000 = -7 · 1000 = -7000
-10² = 100
-8 · 100 = -800
-7000 - 800 - 26 = -7800 - 26 = -7826
ответ: -7826
3 было вначале.
После того, как отрубили голову
в 1-й раз: (3-1) + 5 = 7
во 2-й раз : 7-1) + 5 = 11
в 3-й раз: (11-1) + 5 = 15
И т.д.
Последовательность выглядит так
7, 11, 15, ... 59, 63
Это арифметическая прогрессия.
an = a1 + d(n - 1) - формула n-го члена арифметической прогрессии.
Здесь
а1 = 7
аn = 63
d = 4, поскольку а2 - а1 = 11 - 7 = 4 и т.п.
Можно найти n - количество членов арифметической прогрессии, которое в данном случае показывает, сколько раз происходило одновременно изменение количества голов дракона.
63 = 7 + 4(n-1)
4(n-1) = 63 - 7
4n - 4 = 56
4n = 56 + 4
4n = 60
n = 60 : 4
n = 15 - столько раз отрубали голову дракону.
ответ: 15 раз.
Проверка:
1. (3-1) + 5 = 7
2. (7-1) + 5 = 11
3. (11-1) + 5 = 15
4. (15-1) + 5 = 19
5. (19-1) + 5 = 23
6. (23-1) + 5 = 27
7. (27-1) + 5 = 31
8. (31-1) + 5 = 35
9. (35-1) + 5 = 39
10 (9-1) + 5 = 43
11. (43-1) + 5 = 47
12. (47-1) + 5 = 51
13. (51-1) + 5 = 55
14. (55-1) + 5 = 59
15. (59-1) + 5 = 63