AB = 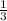
BC = 1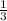
AC = 1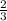
Пошаговое объяснение:
По условию единичный отрезок равен 6 клеткам.
Чтобы найти точку A (2/6), нужно единичный отрезок разделить на 6 частей (получается 1 клетка) и взять 2 таких части (2 клетки соответствуют 2/6).
Аналогично находится точка B.
Точка С имеет координату 12/6, это неправильная дробь, она больше 1. Выделим целую часть: 12/6 = 2. Значит точка C имеет координату = 2.
Длина отрезка на координатном луче измеряется в единичных отрезках. Чтобы найти длину отрезка на координатном луче, нужно найти разность координат концов отрезка.
Решение в приложенном рисунке.

Найдём производную функции: y = x / 3 – 4 /x ^2 + √x.
Эту функцию можно записать так: y = (1 / 3)x - 4x^(- 2) + √x.
Воспользовавшись формулами:
(x^n)’ = n* x^(n-1) (производная основной элементарной функции).
(√x)’ = 1 / 2√x (производная основной элементарной функции).
(с * u)’ = с * u’, где с – const (основное правило дифференцирования).
(u + v)’ = u’ + v’ (основное правило дифференцирования).
Таким образом, производная нашей функции будет следующая:
y' = (x / 3 – 4 /x ^2 + √x)’ = ((1 / 3)x - 4x^(- 2) + √x)’ = ((1 / 3)x)’ – (4x^(- 2))’ + (√x)’ = (1 / 3 ) – (4 * (- 2) * x^(- 2 - 1)) + (1 / 2√x) = (1 / 3 ) + 8x^(- 3)) + (1 / 2√x) = (1 / 3 ) + (8 / x^3) + (1 / 2√x).
ответ: y' = (1 / 3 ) + (8 / x^3) + (1 / 2√x).
Пошаговое объяснение: