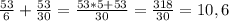м
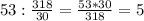дней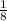
работы, 2-й за день выполнит 
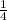. Тогда, работая совместно, они выполнят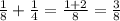 
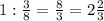дня.ответ просят выразить в часах. Интересно, ведь не круглые сутки они копают. Если формально (хоть это не реально), то в сутках 24 часа 1/3 сут=8ч
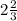сут=
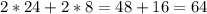часа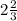 рабочих дня это будет 
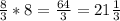часов
Решаю первую задачу. Решу через уравнение двумя уравнением с двумя переменными и одной. Одна переменная: Пусть x- это кол-во продуктов в меньшем рюкзаке, тогда в большем будет 5x. Зная, что, чтобы уровнять груз, 6 кг продуктов из большего рюкзака переложили в меньшей рюкзак, составим и решим уравнение: 5x-6=x+6, 5x-x=6+6, 4x=12,x=3.Если в меньшем рюкзаке было 3 кг продуктов, то в большем будет 5*3=15кг.Выполняем проверку: 15кг-6кг=3+6кг.
Система уравнений с двумя переменными: Пусть x- это кол-во продуктов в первом рюкзаке, а y- кол-во продуктов во вторм рюкзаке. Зная, что в первом рюкзаке продутов было в пять раз больше чем во втором, составим и решим первое уравнение с двумя переменныйми: x=5y. Зная, что из первого рюказка переложили 6 кг продутов во второй, и они стали равны, составим и решим второе уравнение: x-6=y+6. Составим ситему и решим ее подстановки 5y-6=y+6. 4y=12, y=3 кг, находишь больший рюкзак как в первом случае. Вторую задачу решу попозже
3 км/ч
Пошаговое объяснение:
Составляем систему уравнений согласно условию задачи, где:
x - скорость течения реки, км/ч;
y - время, через которое встретились плот и катер после его отправления, ч;
2 ч 40 мин = (2 +40/60) ч = (6/3 +2/3) ч = 8/3 ч - время плота в пути до отправления катера;
8/3 ·x+xy=14
y(12-x)=32-14
x(8/3 +(3y)/3)=14; (3y)/3=14/x -8/3; (3y)/3=(42-8x)/(3x); y=(42-8x)/(3x)
y=18/(12-x)
(42-8x)/(3x)=18/(12-x)
(42-8x)(12-x)=18·3x
504-42x-96x+8x²=54x
8x²-138x+504-54x=0
8x²-192x+504=0 |8
x²-24x+63=0; D=576-252=324
x₁=(24-18)/2=6/2=3; y₁=18/(12-3)=18/9=2
x₂=(24+18)/2=42/2=21; y₂=18/(12-21)=18(-9)=-2 - этот корень не подходит по смыслу задачи, следовательно, корень x₂ также не подходит.
Отсюда следует, скорость течения реки 3 км/ч.