Возьмём эти неизвестные числа за x, тогда получим двойное неравенство:
10,53 < x < 10,55
Теперь, можем написать, что x = 10,54, но это одно число, необходимо найти еще 2.
Вспомним, что помимо сотых частей есть тысячные, десятитысячные, стотысячные и т.д. Чтобы в числах 10,53 и 10,55 сотые части превратить в тысячные, нужно дописать к ним по нулю, получим двойное неравенство:
10,530 < x < 10,550
Теперь найти значение x легко;
, что значит, что x может быть равен 10,531; 10,532; 10,533; 10,534; 10,535; 10,536; 10,537; 10,538; 10,539; 10,541; 10,542; 10,543; 10,544; 10,545; 10,546; 10,547; 10,548; 10,549.
По условию, выпишем только три любые числа, пусть это будут 10,533; 10,534; 10,535.
ответ: 10,533; 10,534; 10,535.
Рассмотрим первое слагаемое (82n). Произведение четного числа на любое другое целое дает нам четное число (правило 2).
Второе слагаемое должно быть нечетным, так как произведение двух нечетных чисел нечетно (правило 1).
И сумма четного и нечетного чисел обязательно нечетна (3), искомое число будет нечетным, что и требовалось доказать!
Примечание:
Необходимые правила:
(1) Если нечетное число умножить на нечетное, то получится тоже нечетное (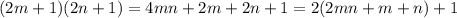
).(2) Произведение четного числа на любое натуральное (или целое) всегда будет четным (если умножаем на нечетное:
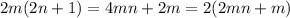; если на четное: 
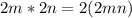).(3) Если сложить четное и нечетное числа, то получится нечетное число (
).
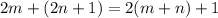Пошаговое объяснение:
a) 1)3 + 4/5 2) 8+7/10 3)25+15/17 4) 4+11/14
б) 4*3\17 18*27/100