Событие B состоит в том, что детали извлечены из 2-й партии
Рассмотрим гипотезы A₁, A₂, A₃, которые состоят из следующих событий
A₁ — детали извлекались из первой партии;
A₂ — детали извлекались из второй партии;
A₃ — детали извлекались из третьей партии.
Вероятность достать детали в каждой партии из трех равна 1/3, т.е.
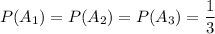
Условная вероятность 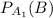 равна 1, так как это событие достоверно, так как в первой партии все детали стандартны.
равна 1, так как это событие достоверно, так как в первой партии все детали стандартны.
Условная вероятность 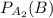 , равна 15/20 = 3/4 — вероятность того, что из второй партии извлечена стандартная деталь.
, равна 15/20 = 3/4 — вероятность того, что из второй партии извлечена стандартная деталь.
Условная вероятность 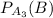 , равна 10/20 = 1/2 — вероятность того, что из третьей партии извлечена стандартная деталь.
, равна 10/20 = 1/2 — вероятность того, что из третьей партии извлечена стандартная деталь.
Вероятность того, что деталь извлечена из второй партии, (по формуле Байеса), равна:
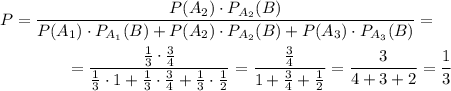
ответ: 1/3.
Событие B состоит в том, что детали извлечены из 2-й партии
Рассмотрим гипотезы A₁, A₂, A₃, которые состоят из следующих событий
A₁ — детали извлекались из первой партии;
A₂ — детали извлекались из второй партии;
A₃ — детали извлекались из третьей партии.
Вероятность достать детали в каждой партии из трех равна 1/3, т.е.
Условная вероятность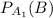 равна 1, так как это событие достоверно, так как в первой партии все детали стандартны.
равна 1, так как это событие достоверно, так как в первой партии все детали стандартны.
Условная вероятность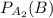 , равна 15/20 = 3/4 — вероятность того, что из второй партии извлечена стандартная деталь.
, равна 15/20 = 3/4 — вероятность того, что из второй партии извлечена стандартная деталь.
Условная вероятность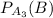 , равна 10/20 = 1/2 — вероятность того, что из третьей партии извлечена стандартная деталь.
, равна 10/20 = 1/2 — вероятность того, что из третьей партии извлечена стандартная деталь.
Вероятность того, что деталь извлечена из второй партии, (по формуле Байеса), равна:
ответ: 1/3.