1) моторная лодка шла со скоростью 11 км/ч
2) муравьишка пробежал до дома 24 м
Пошаговое объяснение:
ДЛЯ ПЕРВОЙ ЗАДАЧИ:
24 часа - 7 часов = 17 часов - время от момента выхода до встречи катера и моторной лодки
за 17 часов со скоростью 19 км/ч катер расстояние в 323 км
(19 км/ч х 17 часов = 323 км)
зная общее расстояние (510 км), можно узнать, какое расстояние моторная лодка: 510-323=187 км,
зная путь моторной лодки можно узнать скорость катера:
путь катера (187) нужно разделить на время (17 часов, т. к. время у них общее), получаем: 187:17=11 км/ч скорость моторной лодки
ДЛЯ ВТОРОЙ ЗАДАЧИ:
пробежал сначала 1/3+8м, осталось пробежать еще 1/2 и 4 м., т.е. половина пути это будет еще 1/3+4м, а еще 1/3 составляют 8+4 м
1/3+8+1/3+4=3/3, значит 1/3 и будет 8+4=12, поэтому сложив 3 раза по 12 получим 24 м
Пошаговое объяснение:
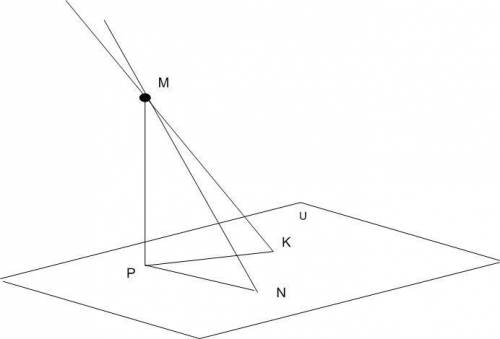
Задача 1. Файл "плоскость"
Дано:
плоскость u;
∠PMK =60°;
l PK l= 8√3;
l MN l=8√2.
Найти:
∠PMN
l PK l / l MP l = tg(∠PMK);
l MP l=l PK l/ tg(∠PMK);
l MP l=8√3/tg60°; tg60°=sin60°/cos60°=(√3/2)/(1/2)=√3;
l MP l=8√3/√3=8;
cos(∠PMN)=l MP l/l MN l;
cos(∠PMN)=8/(8√2)=1/√2=√2/(√2*√2)=√2/2;
∠PMN = arccos(√2/2)=45°
ответ:∠PMN = 45°
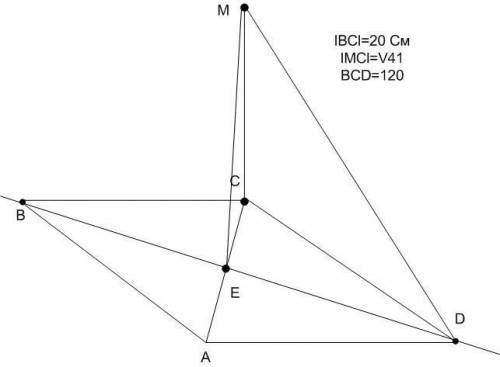
Задача 2. Файл "ромб"
Дано
ABCD - ромб со стороной 20 см
l CD l=20 см
∠BCD=120°
l MC l=√41 см
Найти:
l MD l, l ME l
l MD l=√(l MC l²+ l CD l²);
l MD l=√(√41)²+20²)=√441=21 (см);
Δ CED - прямоугольный, т.к. у ромба диагонали пересекаются под прямым углом.
Сумма углов выпуклого 4-х угольника, а, значит, и ромба - 360°. У ромба противоположные углы равны, значит:
∠CDA=(360°-120-120)/2=60;
Диагональ ромба является биссектрисой противолежащих углов, значит:
∠CDE=∠CDA/2;
∠CDE=60°/2=30°;
В Δ CED l CE l=l CD l*sin(∠CDE);
l CE l=20*sin30°=20*(1/2)=10 (см);
ΔMCE- прямоугольный.
l ME l=√(l CE l²+l MC l²);
l ME l=√(10²+(√41)²)=√141.
ответ: l MD l=21 см, l ME l =√141 см
305 003 065 003 вот
Пошаговое объяснение: