√26sin(α+π/2), если ctgα=-5 , 0°<α<180°. Не могу понять как выбрать знак при косинусе ведь он лежит между 180 и 0
Пошаговое объяснение:
{ctgα=-5 ( котангенс отрицателен во 2и 4 четвертях)
{ 0°<α<180° ( это 1 и 2 четверти)
Из этих двух условий следует , что α∈ II четверти. Во 2 четверти cosα<0.
√26sin(α+π/2)= √26cosα
Т.к 1+ctg²α=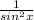
, то 1+(-5)²=
, sin²α=1/26.
По основному тригонометрическому тождеству
sin²α+cos²α=1
1/26+cos²α=1
cos²α=1-1/26
cos²α=25/26
cosα= -√(25/26) , cosα= -5/√26.
√26sin(α+π/2)= √26cosα= √26*(-5/√26)= -5
Наибольшая высота равна 24 см
Наибольшая высота проходит к меньшей стороне.
Найдём лощадь треугольника по формуле Герона:
S=√(p*(p-a)*(p-b)*(p-c)), где р - полупертметр
р= 1/2*(25+26+3)=27
S=√(27*(27-26)*(27-25)*(27-3)) =√(27*2*24)=√1296=36
Площадь треугольника через основание и высоту:
S=1/2*a*h
Следовательно, формула высоты: h=2*S/a
h=2*36/3
h=24
1) 3 и 4
2) 36 см²
3) В треугольнике наибольшая та сторона, которая проведена к наименьшей стороне