Question

Какие из пар (-2; 4); (-1; -3; (3; 4) является решением системы: всем свои (есле можно то фотографию пришлите ато я ничего непойму)​мне нужно успеть до 29 апреля, до школы.

Answer 1

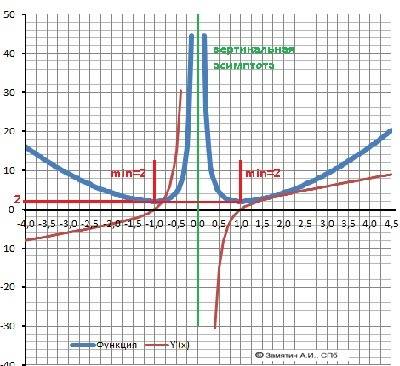
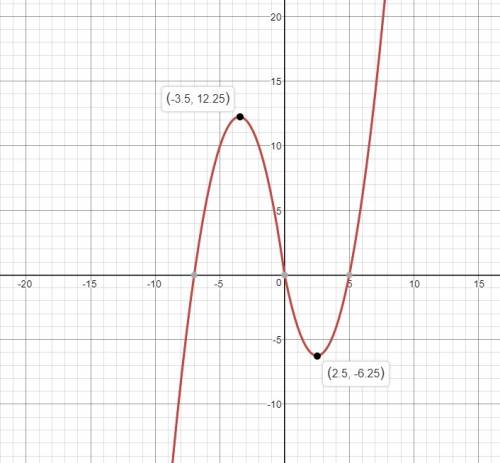
ответ: 1) (-2; 4),  2) (3; 4).

Пошаговое объяснение:

Чтобы узнать, является ли пара чисел решением системы, необходимо их подставить в уравнения системы. Если оба равенства будут верными, то пара чисел является решением, в противном случае не является.

В паре (a, b) первое число -- это значение x, а второе -- y.

$1) \left\{\begin{matrix}5x-y+14=0,\\ x+2y-6=0.\end{matrix}\right.$

Подставляем в каждое уравнение пару чисел (-2; 4) (то есть x = -2, y = 4):

$5x-y+14=0 \;\;\Rightarrow\;\;5\cdot(-2)-4+14=0\;\;\Rightarrow\;\;0=0\\ x+2y-6=0 \;\;\Rightarrow\;\;-2+2\cdot4-6=0\;\;\Rightarrow\;\;0=0$

Оба равенства верные, следовательно, пара чисел (-2; 4) является решением системы 1).

Проверим пару чисел (-1; -3):

$5x-y+14=0 \;\;\Rightarrow\;\;5\cdot(-1)-(-3)+14=0\;\;\Rightarrow\;\;12\neq 0$

Первое уравнение дало неверное равенство, следовательно, пара чисел (-1; -3) не является решением системы 1).

Проверим пару чисел (3; 4):

$5x-y+14=0\;\;\Rightarrow\;\;5\cdot3-4+14=0\;\;\Rightarrow\;\;25\neq0$

Пара чисел (3; 4) не является решением системы 1).

$2)\left\{\begin{matrix}4x-y-8=0,\\ x-y+1=0.\end{matrix}\right.$

Проверим пару чисел (-2; 4):

$4x-y-8=0\;\;\Rightarrow\;\;4\cdot(-2)-4-8=0\;\;\Rightarrow\;\;-4\neq0$

Пара чисел (-2; 4) не является решением системы 2).

Проверим пару чисел (-1; -3):

$4x-y-8=0\;\;\Rightarrow\;\;4\cdot(-1)-(-3)-8=0\;\;\Rightarrow\;\;-9\neq0$

Пара чисел (-1; -3) не является решением системы 2).

Проверим пару чисел (3; 4):

$4x-y-8=0\;\;\Rightarrow\;\;4\cdot3-4-8=0\;\;\Rightarrow\;\;0=0\\ x-y+1=0\;\;\Rightarrow\;\;3-4+1=0\;\;\Rightarrow\;\;0=0$

Пара чисел (3; 4) является решением системы 2).