Пусть х (км) - длинна пассажирского поезда, тогда 2х (км) - длина товарного поезда.
1) 80-60=20 (км/ч) - скорость обгона
4,5 мин. = 0,075 ч
2) 20*0,075= 1,5 (км) - длина пути, за которое происходил обгон
Начало обгона было в тот момент, когда голова пассажирского достигла хвоста товарного, а конец обгона - когда хвост пассажирского миновал голову товарного. Тогда, нарисовав чертеж, Вы увидите, что длина этого обгона (т.е. путь, проходимый пассажирским за время обгона) равна сумме длин обоих поездов, т.е. утроенной длине пассажирского (т.е. длина обгона = 3х)
3) 3х=1,5
х= 0,5 (км)
х= 500 (м)
ответ: 500 м
Решением неравенства 48 - 13х - х² ≥ 0 есть множество чисел [-16;3] , в котором содержится 20 целых чисел.
а) из этих двадцати чисел только 3 удовлетворяют неравенству х²>0 (1, 2 и 3), значит вероятность будет равна 3/20
б) решением неравенства х² + 10х ≤ 0 есть множество чисел [-10;0] , в котором содержится 11 целых чисел. Все они попадают во множество [-16;3] . Вероятность равна 11/20
в) решением неравенства х² < 101 есть множество чисел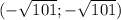
, в котором содержится 21 целое число, из которых 14 попадают во множество [-16;3] (числа от -10 до 3) . Вероятность равна 14/20 = 7/10
г) решением неравенства 4х² - 20х + 21 < 0 есть множество чисел (1,5; 3,5) , в котором содержится 2 целых числа (2 и3), оба попадают во множество [-16;3]. Вероятность равна 2/20 = 1/10