Так как не сказано, с какой стороны будет касание, то решений будет 2.
Так как заданная прямая, к которой будет касание, вертикальна, то центр окружности будет левее и правее её на величину радиуса, то есть появилось ещё одно условие расположения центра окружности.
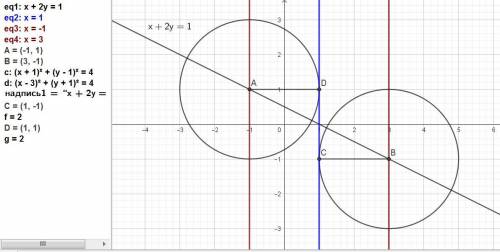
Это будут прямые х = 1 - 2 = -1 и х = 1 + 2 = 3.
Находим координаты центров окружностей как точки пересечения заданной прямой x+2y-1=0 и двух найденных х = -1 и х = 3.
Подставляем значения х в уравнение прямой x+2y-1=0.
-1 + 2у -1 = 0,
2у = 2, у = 2/2 = 1.
Один центр найден: А(-1; 1).
Аналогично находим:
3 + 2у -1 = 0,
2у = -2, у = -2/2 = -1.
В(3; -1).
ответ: (x + 1)² + (y - 1)² = 2².
(x - 3)² + (y + 1)² = 2².
.
Задуманное число примем за единицу (целое).
1) 1 : 2 = 1/2 - половина задуманного числа;
2) 1 : 7 = 1/7 - седьмая часть задуманного числа;
3) 1/2 - 1/7 = 7/14 - 2/14 = 5/14 - часть числа, равная 80;
4) Находим целое по его части:
80 : 5/14 = (80 : 5) · 14 = 16 · 14 = 224 - задуманное число.
.
Пусть х - задуманное число, тогда 1/2х - половина задуманного числа, 1/7х - седьмая часть задуманного числа. Уравнение:
1/2х - 1/7х = 80
7/14х - 2/14х = 80
5/14х = 80
х = 80 : 5/14
х = 80/1 · 14/5
х = 16 · 14
х = 224
ответ: 224 - задуманное число.
Проверка:
1/2 · 224 = 224 : 2 = 112 - половина задуманного числа
1/7 · 224 = 224 : 7 = 32 - седьмая часть задуманного числа
112 - 32 = 80 - разница (по условию задачи)
не знаю
Пошаговое объяснение: