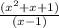
Пошаговое объяснение:
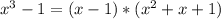
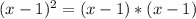
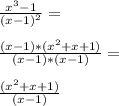
Луч, построенный таким называется координатным или числовым. Начало числового луча, точка О, называется точкой отсчета. Числа, поставленные в соответствие точкам на этом луче, называются координатами этих точек (отсюда: координатный луч). Пишут: О(0), А(1), В(2), читают: «точка О с координатой 0 (ноль), точка А с координатой 1 (один), точка В с координатой 2 (два)» и т.д.
Любое натуральное число n можно изобразить на координатном луче, при этом соответствующая ему точка P будет удалена от точки О на n единиц. Пишут: ОP = n и P(n) - точка P (читают: "пэ") с координатой n (читают: "эн"). Например, чтобы отметить на числовом луче точку К(107), необходимо от точки О отложить 107 отрезков, равных единичному. В качестве единичного можно выбрать отрезок любой длины. Часто длину единичного отрезка выбирают такой, чтобы было возможно в пределах рисунка изобразить на числовом луче необходимые натуральные числа
Пошаговое объяснение:
7,8-(-6,9)=7,8+6,9=14,7
-6,7-(-7,6)= - 6,7+7,6=7,6-6,7=0,9
- 5,4-6,8= - (5,4+6,8)= - 12,2
Этот пример: написано (20 3/4), а в пояснении ( - 20 3/4). Делаю оба.
- 15 4/5 - (-20 3/4)= - 15 16/20+20 15/20=20 15/20 - 15 16/20=4 19/20
- 15 4/5 - 20 3/4= - (15 16/20+20 15/20)= - 35 31/20= - 36 11/20
16/21 - 5 1/3=16/21 - 5 7/21= -(5 7/21 - 16/21)= -(4 28/21 - 16/21)= - 4 12/21= - 4 4/7
.
2 1/2 - 3 1/3=2 3/6 - 3 2/6= - (2 8/6 - 2 3/6)= - 5/6
- 3/5 - 1 1/3= - (9/15+1 5/15)= - 1 14/15
5 7/8 - ( - 2 5/12)=5 21/24+2 10/24=7 31/24=8 7/24
- 2 3/4 - (- 4/7)= - 2 21/28+16/28= - (2 21/28 - 16/28)= - 2 5/28
- 4 11/12 - ( - 11/18)= - 4 33/36+22/36= - (4 33/36 - 22/36)= - 4 11/36
х^3 -1=(x-1)(x^2+x+1)
x-1 сокращается
остается х^2+x+1
Пошаговое объяснение: