ответ:1. Рассмотрим △OAR: ∠OAR = 90° (так как OA — высота), ∠AOR = 15° (по условию).
По теореме о сумме углов треугольника: сумма всех внутренних углов любого треугольника равна 180°. Тогда, для △OAR:
∠OAR + ∠ARO + ∠AOR = 180°;
90° + ∠ARO + 15° = 180°;
∠ARO = 180° - 90° - 15°;
∠ARO = 75°.
2. В прямоугольнике MRKH пары сторон MR и KN, MN и RK параллельны (по определению прямоугольника)
∠ARO = ∠ONK так как они являются накрест лежащими углами, образованными при пересечении параллельных прямых MR и KN секущей RN.
Таким образом, ∠ONK = 75°.
ответ Пошаговое объяснение:
1. Рассмотрим △OAR: ∠OAR = 90° (так как OA — высота), ∠AOR = 15° (по условию).
По теореме о сумме углов треугольника: сумма всех внутренних углов любого треугольника равна 180°. Тогда, для △OAR:
∠OAR + ∠ARO + ∠AOR = 180°;
90° + ∠ARO + 15° = 180°;
∠ARO = 180° - 90° - 15°;
∠ARO = 75°.
2. В прямоугольнике MRKH пары сторон MR и KN, MN и RK параллельны (по определению прямоугольника)
∠ARO = ∠ONK так как они являются накрест лежащими углами, образованными при пересечении параллельных прямых MR и KN секущей RN.
Таким образом, ∠ONK = 75°.
ответ
В классе всего 12 + 18 = 30.
1) Вероятность выбрать первого мальчика равна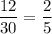 
. Одного человека мы выбрали уже, тогда в классе остается 11 мальчиков и 18 девочек. Вероятность выбрать второго мальчика равна 
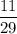. По теореме умножения, искомая вероятность: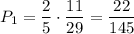 
2) Выбрать первую девочку можно с вероятностью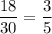 
. В классе остается 29 человек из них 17 девочек. Вероятность выбрать вторую девочку равна 
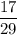. По теореме умножения, искомая вероятность: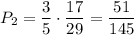 
3) Вероятность того, что среди двух выбранных человек окажутся девочка и мальчик, равна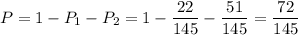 
ответ: 1) 22/145; 2) 51/145; 3) 72/145.
Відповідь: 13см
Пояснення: