Question

Постройте график функции y=x|x|+2|x|-5x . определите , при каких значениях m прямая y=m имеет с графиком ровно две общие точки

Answer 1

$y=x|x|+2|x|-5x\\\left[\begin{array}{cc}\left \{ {{x\geq 0} \atop {y=x^2-3x}} \right. \\\left \{ {{x\leq 0} \atop {y=-x^2-7x}} \right. \end{array}$

y=x²-3x.

Это парабола, ветви которой вверх. Найдём точки пересечения с осями координат: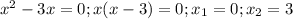 $x^2-3x=0;x(x-3)=0;x_1=0;x_2=3$ (0;0) и (3;0)

$y=0^2-3*0=0$ (0;0).

Вершина параболы: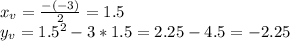 $x_v=\frac{-(-3)}{2} =1.5\\y_v=1.5^2-3*1.5=2.25-4.5=-2.25$ (1.5;-2.25)

y=-x²-7x

Это парабола, ветви которой вниз. Найдём точки пересечения с осями координат: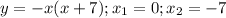 $y=-x(x+7);x_1=0;x_2=-7$ (-7;0) и (0;0)

$y=((-0)^2-7*0)=0$ (0;0).

Вершина параболы: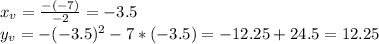 $x_v=\frac{-(-7)}{-2} =-3.5\\y_v=-(-3.5)^2-7*(-3.5)=-12.25+24.5=12.25$ (-3.5;12.25)

Сначала построим графики отдельно, отметим ограничение и построим в общей системе координат.

Прямая y=m, это прямая, которая параллельна оси Ох, по графику функции видно, что сначала 1 пересечение, потом 2, затем 3, опять 2 и снова 1 пересечение. Две общие точки, когда два пересечения, а именно в вершинах, парабол, которые мы строили до этого, нам нужно значение по ординате, поэтому берём -2.25 и 12.25.

ответ: m={-2.25;12.25}